5.2.7. Поверхности второго порядка

Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:

– уравнению второй степени от трех неизвестных, называемому Общим уравнением поверхности второго порядка.

Если найти собственные числа и нормированные собственные векторы матрицы квадратичной формы

И перейти к системе координат, определяемой базисом из ортонормированных собственных векторов, уравнение (6) можно привести к одному из следующих видов:

1. Если L1, L2, L3 – одного знака, уравнение (6) есть уравнение эллиптического типа и приводится к канонической форме:

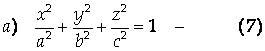
Каноническое уравнение Эллипсоида.

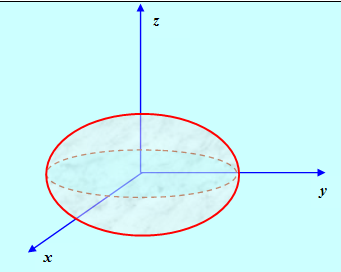
Рис. 4

Замечание. Если два собственных числа совпадают, эллипсоид называется эллипсоидом вращения и представляет собой поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Если все собственные числа равны, уравнение (7) становится уравнением сферы.

Уравнение задает Точку в пространстве;

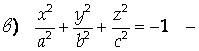
Пустое множество.

2. Если собственные числа разных знаков, уравнение (12.6) приводится к каноническому виду:

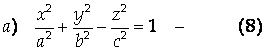
Каноническое уравнение Однополостного гиперболоида,

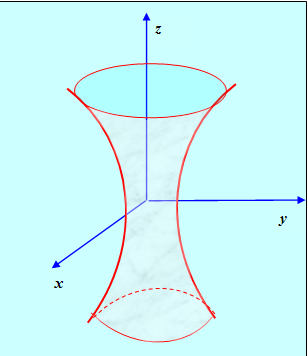
Рис. 5

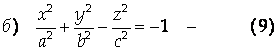
Каноническое уравнение Двуполостного гиперболоида,

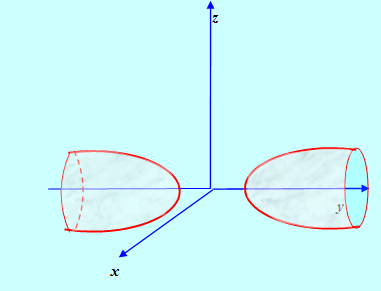
Рис. 6

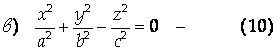
Уравнение Конуса второго порядка.

Рис. 7

3. Одно из собственных чисел равно 0. При этом с помощью преобразований координат можно получить следующие формы уравнения (6):

Каноническое уравнение Эллиптического параболоида,

Рис. 8

Каноническое уравнение Гиперболического параболоида

Рис. 9

И уравнения цилиндрических поверхностей:

Эллиптический цилиндр,

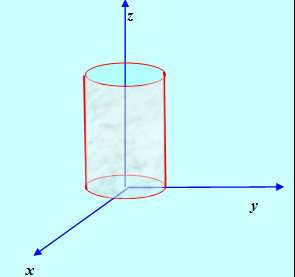
Рис. 10

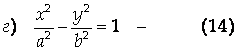
Гиперболический цилиндр.

Рис 11

Наконец, уравнение может определять Пару плоскостей:

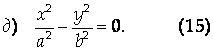
Рис. 12

4. Если два собственных числа равны 0, уравнение (6) приводится к одному из следующих видов:

Параболический цилиндр,

Пара параллельных плоскостей,

Пустое множество.

< Предыдущая		Следующая >