5.2.6. Классификация кривых второго порядка

Рассмотрим общее уравнение второго порядка (4):

И выясним, какие геометрические образы на плоскости могут задаваться этим уравнением.

1. Если собственные числа матрицы А L1 и L2 одного знака, уравнение (4) называется уравнением Эллиптического типа. Его можно привести к виду (5):

Которое, в свою очередь, преобразуется в следующую форму:

А) если Имеет тот же знак, что и L1,2, при делении на Получаем

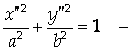
Каноническое уравнение Эллипса.

Б) если =0, уравнение

Имеет единственное решение:

Определяющее Точку на плоскости.

В) если знак противоположен знаку L1,2, уравнение после деления на примет вид:

Множество его решений пусто (иногда это пустое множество называют Мнимым эллипсом).

2. Если собственные числа матрицы А L1 и L2 разных знаков, уравнение (4) называется уравнением Гиперболического типа.

А) при оно сводится к одному из двух видов:

В зависимости от знака . Оба этих уравнения определяют Гиперболу.

Б) При =0 получаем уравнение

Эквивалентное двум линейным уравнениям:

Задающим Пару пересекающихся прямых.

3. Если одно из собственных чисел равно 0, уравнение (4) называется уравнением Параболического Типа, и его можно привести к одному из следующих видов:

А) к уравнению

Определяющему Параболу;

Б) к уравнению

Задающему Пару параллельных прямых;

В) к уравнению

Определяющему Одну прямую (или пару совпадающих прямых);

Г) к уравнению

Не имеющему решений и, следовательно, не определяющему никакого геометрического образа.

< Предыдущая		Следующая >