5.1.1. Линейные операторы и кривые 2-го порядка. Линейные операторы

Будем говорить, что на множестве векторов R задан Оператор А, если каждому вектору ХR По некоторому правилу поставлен в соответствие вектор АХR.

Оператор А Называется Линейным, если для любых векторов Х и У и для любого действительного числа L выполняются равенства:

Линейный оператор называется Тождественным, если он преобразует любой вектор Х В самого себя. Тождественный оператор обозначается Е: ЕХ = Х.

Рассмотрим трехмерное пространство с базисом Е1, Е2, Е3, в котором задан линейный оператор А. Применив его к базисным векторам, мы получим векторы АЕ1, АЕ2, АЕ3, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:

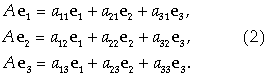
Матрица

Называется Матрицей линейного оператора А в базисе Е1, Е2, Е3 . Столбцы этой матрицы составлены из коэффициентов в формулах (2) преобразования базиса.

Замечание. Очевидно, что матрицей тождественного оператора является единичная матрица Е.

Для произвольного вектора Х =х1Е1 + х2Е2 + х3Е3 результатом применения к нему линейного оператора А будет вектор АХ, который можно разложить по векторам того же базиса:

Где координаты X`I можно найти по формулам:

Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.

< Предыдущая		Следующая >