4.1.8. Примеры решения задач по теме «Уравнение прямой на плоскости»

Задача 1.

Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у - 3 = 0. Найти координаты вершин этого параллелограмма.

Указание

Выясните, уравнения каких сторон даны в условии задачи: параллельных или

Смежных, и как расположена данная диагональ по отношению к данным сторонам.

Решение

Рис. 12

Выясним, уравнения каких сторон даны в условии задачи: параллельных или

Смежных.

Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.

Условие параллельности прямых

А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0:

Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:

Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:

Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.

Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:

Система уравнений для определения координат точки D составлена из уравнений прямых AD И BD:

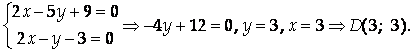
Остается найти координаты точки С. Составим уравнения прямых ВС и DC.

Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:

Тогда ВС можно задать уравнением

Аналогично АВ: У = -2Х – 3, KAB = -2 = KDC; DC: Y – 3 = -2(X – 3), 2X + Y – 9 = 0.

Найдем координаты точки С, решив систему из двух полученных уравнений:

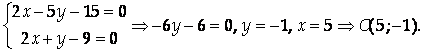
Ответ: А(1; -2), В(0; -3), С(5; -1), D(3; 3).

Задача 2.

Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).

Указание

Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:

1) провести прямую ВС;

2) провести через точку А прямую, перпендикулярную ВС;

3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.

Решение

Рис. 13

Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:

4) провести прямую ВС;

5) провести через точку А прямую, перпендикулярную ВС;

6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.

Тогда точка А1 будет симметричной точке А относительно прямой ВС.

Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.

1) Найдем уравнение прямой ВС в виде:

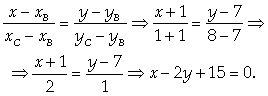
2) Найдем угловой коэффициент прямой ВС:

Прямая АО Перпендикулярна прямой ВС, поэтому

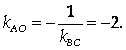
Составим уравнение прямой АО:

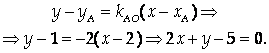
3) Найдем координаты точки О как решение системы:

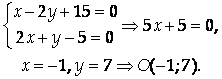
4) Точка О – середина отрезка АА1, поэтому

Ответ: (-4; 13).

Задача 3.

Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.

Указание

Если J – угол между прямыми L1 и L2, то J = A2 - A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда

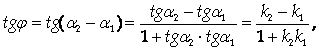
Где K1 и K2 – угловые коэффициенты прямых L1 и L2.

Решение

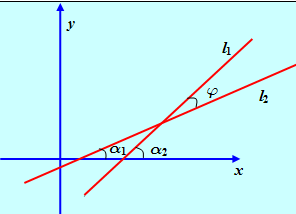
Рис. 14

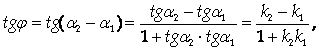
Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1

Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,

Ответ: 45о.

Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0

Справедлива формула:

Задача 4.

Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.

Указание

Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.

Решение

Рис. 15

Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:

Для ответа на вопрос задачи отметим, что:

1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);

2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).

Составим нормальные уравнения сторон треугольника АВС:

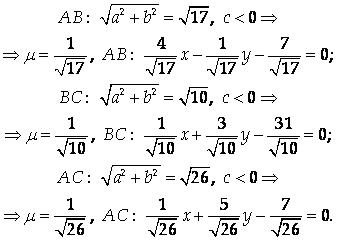
Вычислим соответствующие отклонения:

1) для точек М и А относительно прямой ВС:

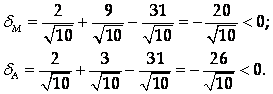
2) для точек М и В относительно прямой АС:

3) для точек М и С относительно прямой АВ:

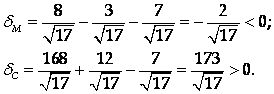
Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.

Ответ: Точка М расположена вне треугольника АВС.

Задача 5.

Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.

Указание

Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.

Решение

Рис. 16

1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:

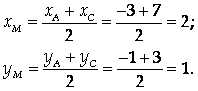
Тогда уравнение медианы можно записать в виде:

2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:

Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.

Задача 6.

Определить, при каком значении А прямая

(А – 5)Х + (А2 – 1)У + 2А2 + 7А – 9 = 0

Параллельна оси ординат. Написать уравнение прямой.

Указание

Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0

В = 0, С ≠ 0.

Решение

Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0

В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.

При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).

При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.

Ответ: 3Х + 7 = 0 при А = -1;

Задача 7.

Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.

Указание

Составьте уравнение искомой прямой «в отрезках»:

Где |A| и |B| - длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».

Решение

Рис. 17

Составим уравнение искомой прямой «в отрезках»:

Где |A| и |B| - длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:

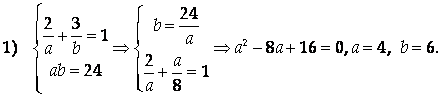
Следовательно, условию задачи удовлетворяют три прямые:

Ответ:

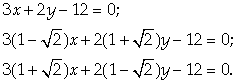
< Предыдущая		Следующая >
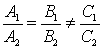