4.1.7. Отклонение и расстояние от точки до прямой

Обозначим через D расстояние от точки М до прямой L. Отклонением точки М от прямой L называется число D, если М и начало координат О лежат по разные стороны от прямой L, и число –D, если М и О лежат по одну сторону от L. Если О принадлежит L и П = (cos J, sin J) – нормальный вектор прямой L, то отклонение положим равным D, когда М лежит по ту же сторону от L, куда направлен вектор П, и –D – в противном случае.

Рис. 11

Пусть Q – проекция точки М = {X, Y} на ось, определяемую вектором П. Тогда отклонение точки М от прямой L равно

Поэтому

Отсюда

В силу того, что D = |D |, имеем

Пример 5. Даны координаты вершин треугольника А = {0,1}, B = {2,1} и C = {3,-1}. Найти длину высоты H, проведенной из вершины В на сторону АС.

Длина высоты равна расстоянию от точки В до прямой, проходящей через точки А и С. Найдем уравнение прямой, проходящей через эти точки:

Приведем это уравнение к нормальному виду:

Следовательно,

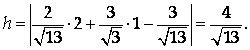
Упражнение 3. Найти расстояние от точек М1 = {-1,3} и М2 = {2,1} до прямой

3Х – 4У + 1 = 0

И выяснить, лежат ли эти точки по одну сторону от прямой или по разные стороны.

Решение.

Приведем уравнение прямой к нормальному виду:

И найдем отклонения данных точек от прямой:

Тогда

А поскольку отклонения точек от прямой имеют разные знаки, точки расположены по разные стороны от прямой.

Ответ: точки расположены по разные стороны от прямой.

< Предыдущая		Следующая >