1.1.2. Сумма матриц

Суммой двух матриц одинакового размера А = ||Aij|| и B = ||Bij|| называют матрицу С = ||СIj|| размера такую, что , .

Пример 1.

.

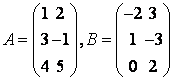
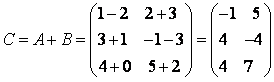Упражнение 3.

Даны матрицы

, .

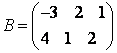Найти А+В.

Нулевой матрицей называется матрица, все элементы которой равны нулю.

Легко проверить, что выполнены следующие свойства для операции сложения матриц:

1. А+В=В+А (коммутативность), 2. (А+В)+С=А+(В+С) (ассоциативность), 3. А+0=А.

Произведением матрицы размера Т5П А = ||Aij|| На число L называют матрицу того же размера С = ||СIj|| такую, что , .

Упражнение 4.

Дана матрица

.

Найти матрицу С= -3А.

Решение.

Из определения произведения матрицы на число следует, что размер матри-цы С совпадает с размером матрицы А (), а каждый элемент матрицы С равен соответствующему элементу матрицы А, умноженному на -3:

Таким образом,

.

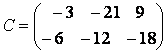Ответ: .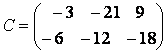

Нетрудно убедиться, что имеют место следующие свойства:

1. L (А+В)= LА+LВ, 2. (L+M)А=LА+MА, 3. (LM)А=L (MА).

Разностью матриц одинакового размера А и В называется матрица А-В=А+(-1)В.

< Предыдущая		Следующая >