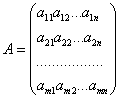1.1.1. Матрицы. Операции над матрицами. Определение матрицы

1.

Матрицей А Размера Называется таблица из Т·п чисел

Часто для краткости пишут А = ||Aij||. Числа, из которых состоит матрица, называются Элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент А23 находится на пересечении второй строки и третьего столбца:

Элементы А11, А22, А33, … называются Главной диагональю матрицы

Если матрица А имеет размер то такую матрицу называют Квадратной матрицей порядка П.

Две матрицы одинакового размера А = ||Aij|| и B = ||Bij|| называют Равными (при этом пишут А = В), если

.

Упражнение 1.

.

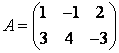Найти А12 и А23.

Решение.

Элемент А12 располагается в первой строке и втором столбце, то есть это второй элемент первой строки: А12 = -1.

Соответственно А23 – элемент, стоящий во второй строке и в третьем столбце;

А23 = -3.

Упражнение 2.

Даны матрицы

.

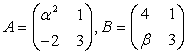При каких A и B А=В?

Решение.

У равных матриц должны быть равными соответствующие элементы. Для элементов, заданных численно, это условие выполняется: A12 = B12 = 1,

A22 = B22 = 3. Поскольку B11 = 4, a A21 = -2, для равенства матриц А и В должны выполняться условия:

.

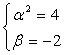Следовательно, A = ±2, B = -2.

Ответ: A = ±2, B = -2.

< Предыдущая		Следующая >