27.Представление невырожденного линейного оператора в виде произведения самосопряженного и унитарного (ортогонального) операторов
Пусть ![]() - произвольный линейный невырожденный оператор, где V=U или V=E; A* - оператор, сопряженный к оператору А.
- произвольный линейный невырожденный оператор, где V=U или V=E; A* - оператор, сопряженный к оператору А.
Лемма: Линейный оператор A*A(так же как AA*) является самосопряженным при этом его собственные значения положительны.
Доказательство:
Введем обозначение B= A*A. Запишем B*=(A*A)*=A*(A*)*= A*A (по свойствам сопряженного оператора 1-му и 2-му) следовательно, B*=B т. е. В – самосопряженный оператор.
Пусть λ - собственное значение оператора В, Х – соответствующий собственный вектор оператора В т. е. Bx= λX, ![]() кроме того
кроме того ![]() По свойству 2 самосопряженных операторов. Тогда
По свойству 2 самосопряженных операторов. Тогда ![]() , отсюда
, отсюда 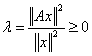 , здесь
, здесь ![]() .
.
Пусть λ=0, тогда ![]() , т. е. Ax=θ и По свойству 40 невырожденных операторов имеем X=θ чего быть не может, т. к.
, т. е. Ax=θ и По свойству 40 невырожденных операторов имеем X=θ чего быть не может, т. к. ![]() #.
#.
Теорема: Любой невырожденный линейный оператор в унитарном (евклидовом) пространстве представим в виде произведения 2-х операторов: самосопряженного и унитарного (ортогонального).
Доказательство: Без доказательства.
Замечание: Самосопряженные и унитарные (ортогональные) операторы достаточны для описания всего множества невырожденных операторов в унитарном (евклидовом) пространстве.
| < Предыдущая | Следующая > |
|---|