21.Спектральная теорема для нормальных операторов и нормальных матриц

Лемма:

Пусть E – собственный вектор нормального оператора A: U → U, – лин. оболочка данного собственного вектора. Тогда 1) ; 2) и явл-ся подпространствоми, инвариантными относительно операторов A И .

Доказательство:

1. Пусть – лин. оболочка собств. вектора E Нормального оператора A: U →U. Тогда по теореме о разложении евклидова (унитарного) пространства в прямую сумму (См.§5 гл. VI). Можно записать, что (отметим, что в §4 гл. III было доказано, что линейная оболочка – подпространство данного линейного пространства).

2. Пусть , т. е. существует : , тогда , используя Св-во 3 норм. Операторов , запишем: . , т. е. – подпространство, инвариантное относительно оператора A.

Пусть , тогда , запишем следовательно .

след-но , т. е. – подпространство, инвариантное, относительно операторов A и . #

Спектральная теорема:

1) Пусть A – норм. оператор, действующий в унитарном протсранстве U. Тогда в пространстве существует ОНБ – базис из собственных вект-ов оператора A.

2) Пусть – нормальная матр. Тогда существует унитарная матр. , столбцами кот. явл-ся собств. в-ры матр. A: такая, что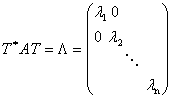

Доказательство:

1) Как всякий линейный оператор, действующий в унитарном (комплексном пространтсве, нормальный оператор A имеет хотя бы одно собственное значение. Пусть и пусть , – линейная оболочка собств. в-ра , отвечающего соб. зн-ю . Тогда в силу суммы , где –

(N-1)мерное подпространство, инвариантное относительно оператора A, т. е. если , то . Рассмотрим теперь норм. оператор A в подпространстве . Тогда точно также существует . Т. к. , то кроме того, можно записать в силу леммы, что , где –

(n-2)мерное подпространство, инвариантное относительно оператора A. Теперь можно записать, что , при этом . Продолжая аналогично этот процесс в конце концов получаем, что при этом , где – ортонормированная сист. собств. В-в норм. оператора A, отвечающая с. знач-ям таким образом, получим ОНБ из собственных в-в нормального оператора A в унитарном пространстве .

2) Пусть – норм. матр. В Унитарн. пространстве выберем произвольный ОНБ . Тогда в этом базисе данной нормальной матр. соотвествует единственный норм. оператор A (по теор. о взаимооднозначном соответствии между линейными операторами и квадратными матрицами и по св-ву 5 норм. операторов). Согласно 1-ой части данной теоремы в унит. пространстве U существует ОНБ из собственных в-в норм. оператора A: . В этом базисе , как известно (см. теор. 1 §7) матр. Оператора имеет диагональный вид

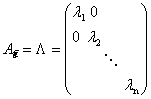причем , где T – матр. перехода от базиса (E) к базису . Матр. T – Унитарная, т. к. явл-ся матр. перехода от одного ОНБ к другому ОНБ (см. св-ва 4 унитарных (ортогональых) матр.), следовательно , т. е. . Наконец по определению матрицы перехода, в столбцах матр. Стоят координаты векторов в базисе (E), т. е. и #

< Предыдущая		Следующая >