11.Норма в евклидовом и унитарном пространствах

Пусть V=E (или V=U)

Определение:

Нормой (или длиной) элемента называется вещественное число

Свойства нормы:

Из свойств скалярного произведения сразу следует:

1) , причем (нулевой элемент)

2)

Доказательство:

#

3) Неравенство Коши-Буяковского

Справедливо

Доказательство:

1. Пусть

А) X=θ, θ, тогда α запишем:

, рассм. левую часть нер-ва как квадратный трехчлен относительно т. к. (y, y)>0,то или

Б) напр., Y = θ, тогда , где θ, откуда .

С другой стороны, нер-во. выполняется (в виде рав-ва)

2. Пусть , тогда C запишем

Пусть, тогда , откуда .

Пусть (здесь ) тогда ,

, рассм. левую часть нер-ва как квадратный трехчлен относительно т. к. (y, y)>0,то #

4) Неравенство треугольника

справедливо:

Доказательство:

Используя неравенство Коши-Буяковского

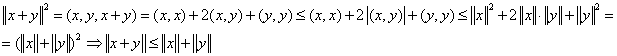
< Предыдущая		Следующая >