08.Теорема (Лагранжа)

Всякая квадратичная форма A(X,X) в вещественном линейном пространстве V при помощи невырожденного линейного преобразования координат может быть приведена к каноническому виду (диагональной форме)., где , а являются координатами вектора X в каноническом базисе т. е. .

Доказательство: (по методу математической индукции) по размерности пространства V , в котором действует .

1) Пусть dimV=1 и E1 - базис в пространстве V, тогда , где , т. е. получили канонический вид.

2) Пусть dimV=M и утверждение доказано.

3) Докажем указанное утверждение при M=N.

Пусть - произвольный базис в Vn, тогда , тогда где .

Возможны два случая:

А) Хотя бы одно из чисел и т. д. отличен от нуля; Пусть, например, (в противном случае проведем перенумерацию базисных векторов). Тогда группируем слагаемые с

Выполним невырожденное преобразование координат:

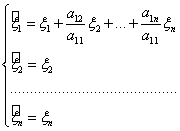или

Получаем: 

2-е слагаемое – квадратичная форма, содержащая (N-1) координат, поэтому по предположению матричной индукции данная квадратичная форма приводится к каноническому (диагональному) виду, т. е. существует невырожденное преобразование координат:

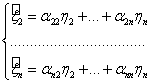, при этом 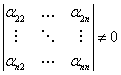и такое, что , поэтому полагая , получаем невырожденное преобразование координат, в результате которого A(X,X) приводится к каноническому виду .

Если T – матрица результирующего преобразования координат, т. е. Или , то .

Б) Пусть теперь все диагональные элементы равны нулю, но отличен от нуля хотя бы один элемент ; Пусть, например, .

Совершим преобразование координат:

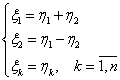
Тогда слагаемое приобретает вид и мы приходим к случаю A) #

Замечание 1: Изложенный в доказательстве последней теоремы метод приведения квадратичной формы к каноническому виду называется методом Лагранжа и фактически сводится к выделению полных квадратов.

Замечание 2: Преобразование переменных, приводящее квадратичную форму A(X,X) к каноническому виду, а значит, и сам канонический базис определяются неоднозначно.

< Предыдущая		Следующая >