План лекции

2. СлУчайные величины

2.1 Дискретные и непрерывные случайные величины

2.2 Закон распределения дискретной случайной величины

2.2.1 Биноминальное распределение

2.2.2 Формула Пуассона

2.3  Законы распределения непрерывных случайных величин

2.3.1 Интегральная функция распределения

2.3.2 Свойства интегральная функция распределения

2.  СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

 

Случайной называется величина, которая при испытаниях принимает одно из возможное значений, наперед неизвестно какое. Неопределенность связана с действием случайных причин, которые не могут быть учтены заранее.

На конкретных примерах можно выделить две группы случайных величин:

Первая группа

Число положительных исходов при

Количество солнечных дней;

Количество пятен на солнце;

Игра в кости;

Лото.

Вторая группа

Ошибки измерений;

Уровень шума в

Электронных приборах.

2.1 Дискретные и непрерывные случайные величины

Дискретной называется случайная величина, которая при испытаниях может принимать одно из изолированных значений, количество которых конечно. К ним относятся величины из первой группы.

Непрерывной  называют случайную величину, которая в пределах ее изменения  может принимать любые значения, которые могут быть конечными или бесконечными. К ним относятся величины из второй группы.

Случайные величины принято обозначать заглавными буквами латинского алфавита:

..., X, Y,Z

Конкретное значение, которое случайная величина (не важно какая – дискретная или непрерывная) приняла при испытании (опыте) принято обозначать как

X1, x2, x3 ,...; y1, y2, y3 ,...; z1, z2, z3,... .

Для дискретной случайной величины принято также обозначать

X = {X1, X2, …, XN },

2.2 Закон распределения дискретных случайных величин

События имеют то свойство, что они либо происходят либо не происходят. Это их свойство можно описать одним числом - вероятностью появления события. Можно представить, что каждое значение хi , которое приобретает величина Х в результате испытаний, это одно из возможных событий Ai и вероятность его появления это pi.

 

Законом распределения случайной величины называется соответствие между значением величины, которое она приняла в результате испытаний, и вероятностью появления этого значения.

Для дискретной случайной величины этот закон может быть описан таблицей:

X	X1	X2	…	Xn
P	P(x1)	P(x2)	…	P(xn)

В одном испытании случайная величина принимает одно и только воз-можное значение. Следовательно, события : “ случайная величина приняла значение xi” составляют полную группу несовместных  6событий:

P1 + p2 + ... + pn = 1

Пример: В денежной лотерее выпущено 1000 билетов. Разыгрывается один выигрыш в 100 гривен, два выигрыша по 50 гривен, десять выигрышей по 10 гривен. Найти: а)- распределение случайной величины Х - суммы выигрыша владельца одного билета; б)- распределение случайной величины У - суммы выигрыша владельца двух билетов.

А) Количество всех возможных вариантов – 1000 или

X	100	50	10	0
P

Б) Количество всех возможных вариантов – 1000 или = 499500

Сумма Выигрыша	150	110	100	60	50	20	10	0
Р

2.2.1  Биномиальное распределение

Пусть производится n испытаний, в каждом из которых событие А может появиться с вероятностью р. Найти распределение вероятностей случайной величины Х, где Х – число появлений событий.

xi = k = 0, 1, 2, …, n. Согласно формуле Бернулли ( см. 1.7.7.1)

;

X	0	1	2	…	N
P				…	Pn

2.2.2  Формула Пуассона

Существуют события, которые имеют весьма малую вероятность появления. Например, p << 0,1. На практике отмечено, что для таких событий при весьма большом количестве испытаний количество положительных исходов практически не зависит от количества произведенных испытвний. В качестве примера можно привести ситуацию, связанную с массовыми перевозками и хранением изделий, когда количество изделий, пришедших в негодность практически не зависит от их общего количества. То-есть

Np = l, n ® ¥ .

Соотношение np = l как раз и  означает, что среднее число появлений маловероятных событий в различных сериях испытаний, т. е. при различных n, остается неизменным.

Так как исходы в каждом из испытаний являются независимыми, то можно использовать формулу Бернулли, полагая, что , а .

.

;

; ;

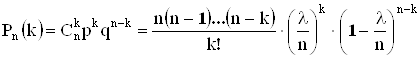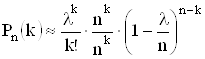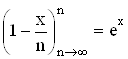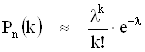- формула Пуассона.

Пример: Установлено, что при транспортировке в вагоне более 5000 изделий портится в среднем одно изделие. Найти вероятность того, что испортится три изделия.

l = 1; k = 3; .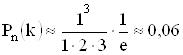

2.3  Законы распределения непрерывных случайных величин

Закон распределения дискретной случайной величины может быть задан таблицей, но такой способ отображения функциональной зависимости не применим для непрерывных случайных величин. Отсюда очевидна целесообразность общего подхода к отображению закона распределения.

2.3.1  Интегральная функция распределения

 

Интегральной функцией распределения называется функция F(x), которая определяет вероятность того, что при испытаниях случайная величина Х примет значение меньше, чем х

.

 

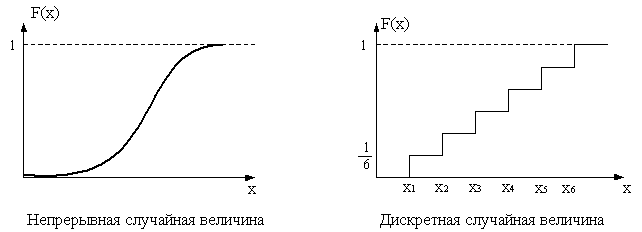
Использование интегральной функции позволяет уточнить понятие “ непрерывная случайная величина”. А именно :

Непрерывной случайной величиной называется случайная величина, у которой функция F(x) непрерывно дифференцируема. Использование интегральной функции распределения позволяет описывать и законы распределения дискретной случайной величины.

2.3.2  Свойства интегральной функции распределения

1. Значения интегральной функции удовлетворяют двойному неравенству:

0≤ F(x)≤ 1

2. F(x) – неубывающая функция.

Следствие 1. Вероятность того, что непрерывная случайная величина примет значение между а и b равна приращению интегральной функции на этом интервале

P(a < x < b)= F(a) – F(b)

Следствие 2. Вероятность того, что непрерывная функция примет одно заранее определеное значение равна 0. Это следует из того, что F(a) – F(а) = 0

3. Если все возможные значения случайной величины принадлежат интервалу (a, b) , то

F(x) = 0; x < a; F(x) = 1; x > b; a = - ¥; b = + ¥; F(-¥) = 0; F(+¥) = 1.

< Предыдущая		Следующая >