Лекция 4
План лекции
1.7.6 Теорема гипотез
1.7.7 Независимые повторные испытания
1.7.7.1 Формула Бернулли
1.7.7.2 Локальная теорема Лапласа
1.7.7.3 Интегральная теорема Лапласа
1.7.6 Теорема гипотез (формула Бейеса)
Эта теорема - следствие теоремы умножения и формулы полной вероятности и позволяет уточнять вероятности появления событий - гипотез от опыта к опыту.
Пусть имеется полная группа событий – гипотез Н1, Н2, … , Нn. Вероятности появлений этих событий, с которыми связано событие А, до проведения опыта известны и равны соответственно: Р(Н1), Р(Н2), …,Р(Нn).
Производится опыт, в результате которого событие A происходит.
Теорема: Если в результате опыта происходит событие А, появление которого определяется гипотезами Н1, Н2, … , Нn, то вероятности этих гипотез изменятся, и эти изменения описываются формулой
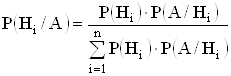 ,
,
Где Р(Нi/А) – апостериорная вероятность I-ой- гипотезы, если событие А произошло
Доказательство:
Согласно теореме умножения вероятность одновременного появления двух событий равна:
P(AHi) = P(A) P(Hi/A) = P(Hi)P(A/Hi) , i =1,2, … , n.
Отсюда P(A) P(Hi/A) = P(Hi) P(A/Hi) , i =1,2, … , n
В этом равенстве P(Hi/A) - условная вероятность события Hi,, рассчитанная при условии, что событие А произошло, а P(A) - это априорная вероятность появления события A, которую находят по формуле полной вероятности:
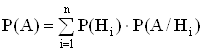 .
.
Пример: На заводе 40% приборов собирают из высококачественных деталей (гипотеза Н1), а 60% - из деталей обычного качества (гипотеза Н2). Вероятность отказа в течение гарантийного срока Q1 = 0,05; Q2 = 0,3. В течение гарантийного срока отказов не произошло. Как изменятся вероятности гипотез Н1 и Н2?
Обозначим событием А отсутствие отказа.
Р(Н1) = 0,4;
Р(Н2) = 0,6;
р1= 1- 0,05 = 0,95 и
р2= 0,7 - соответствующие гипотезам условные вероятности.
Р(А) = Р(Н1)×Р(А/Н1) + Р(Н2)×Р(А/Н2) = 0,4×0,95+0,6×0,7 = 0,38+0,42 = 0,8;
Р(Н1/А) = 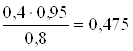 - апостериорная вероятность гипотезы Н1
- апостериорная вероятность гипотезы Н1
Р(Н2/А) = 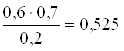 - апостериорная вероятность гипотезы Н2 . Решим задачу для случая, когда отказ произошел ( событие
- апостериорная вероятность гипотезы Н2 . Решим задачу для случая, когда отказ произошел ( событие ![]() ).
).
![]() ;
;
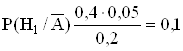 - апостериорная вероятность гипотезы Н1
- апостериорная вероятность гипотезы Н1
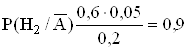 - апостериорная вероятность гипотезы Н2 .
- апостериорная вероятность гипотезы Н2 .
1.7.7 Независимые повторные испытания
|
Испытания называются независимыми, если исход каждого опыта ( событие А произошло или не произошло) не зависит от того, какие исходы имели другие опыты. |
Пусть вероятность появления события А в каждом из этих опытов одна и та же: ![]() и
и ![]() .
.
1.7.7.1 Формула Бернулли
Теорема: Вероятность появления события А ровно k-раз при количестве опытов n определяется количеством возможных комбинаций, при которых событие А происходит. Эта вероятность равна
![]() - формула Бернулли.
- формула Бернулли.
Доказательство:
Предварительно рассмотрим ситуации, возможные при количестве опытов n = 3 для k = 2
![]() ,
,
и ситуации, возможные при количестве опытов n = 4 для k = 3:
![]() .
.
Возможные исходы при любом n для k = 0,1,2,…,n можно найти из выражения:
![]() ,
,
Где индексы соответствуют порядковому номеру испытания. Согласно аксиоме сложения и частному случаю теоремы умножения для независимых событий можно прийти к выводу, что вероятности возможных комбинаций определяются выражением ![]() , которое представляет собой бином Ньютона:
, которое представляет собой бином Ньютона:
![]()
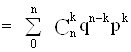 .
.
Пример: Рассчитать вероятность поражения цели 0,1,2,3 раза при пуске трех ракет, если вероятность поражения одной ракетой р = 0,9.
0 ![]() ;
;
1 ![]() ;
;
2 ![]() ;
;
3 ![]() .
.
1.7.7.2 Локальная теорема Лапласа
Эта теорема применима для большого числа испытаний ( n > 20), когда формула Бернулли требует большого количества вычислений.
Теорема Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие A появится в n испытаниях ровно k раз приближенно равна
(см. 2.5.2) 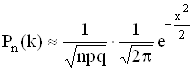 , где 0 ¹ р ¹ 1;
, где 0 ¹ р ¹ 1; 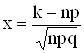 ; n > 20.
; n > 20.
Это выражение может вывести, если использовать формулу Стирлинга, которая дает приближенное значения факториала для больших значений n :
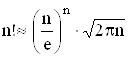
Функция 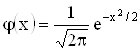 (см. 2.5.5) приводится в таблицах и может быть посчитана с помощью калькулятора.
(см. 2.5.5) приводится в таблицах и может быть посчитана с помощью калькулятора.
Пример. Найти вероятность того, что событие A наступит ровно 80 раз в 400-ах испытаниях, если вероятность появления A в каждом p=0.2.
N = 400 k = 80 p = 0.2 находим х = 0 ![]()
Р400(80) = 0,0498
1.7.7.3 Интегральная теорема Лапласа
В практике применения теории вероятности возникает задача, когда нужно определить вероятность появления события не менее k1 и не более k2 раз при условии, что количество испытаний n достаточно велико.
Пример: Вероятность того, что транзистор не прошел ОТК, равна 0,2. Найти вероятность того, что среди 400 транзисторов не проверено от 70 до 100.
Теорема: Если вероятность события А равна р, и она одинакова в каждом испытании и отлична от 0 и 1, то вероятность события, которое заключается в том, что А происходит от k1 до k2 раз, приближенно равна
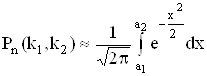 ,
,
где n > 20; 0 ¹ p ¹ 1;  ;
; 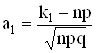 .
.
Функция 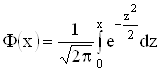 , которая называется интегралом Лапласа (см. 2.5.5) приводится в учебниках и справочниках по теории вероятностей;
, которая называется интегралом Лапласа (см. 2.5.5) приводится в учебниках и справочниках по теории вероятностей;
Рn(k1,k2) = Ф(а2) - Ф(а1).
Вернемся к нашему примеру
p=0.2 q=0.8 n=400 k1 = 70 k2 =100 npq = 82
P400(70,100) = Ф(а2) - Ф(a1) = Ф(2.5) - Ф(-1.25)
P400(70,100) = 0.888
| < Предыдущая | Следующая > |
|---|