Лекция 3
План лекции
1.7.3 Теорема сложения
1.7.4 Теорема о вероятности появления хотя бы одного
из независимых событий
1.7.5 Формула полной вероятности
1.7.3 Теорема сложения
Теорема: Вероятность суммы (любых) двух событий равна сумме вероятностей каждого за вычетом вероятности их совместного появления
Р(А+В) = Р(А) + Р(В) – Р(А×В).
Доказательство:
Представим событие А+В как сумму несовместных событий:
![]() .
.
Используем аксиому о вероятности суммы несовместных событий
![]()
Далее применяем теорему умножения: P(AB) = P(A)P(B/A) = P(B)P(A/B)
![]()
Согласно следствию из аксиомы 4
Можно переписать
![]()
Далее
![]()
![]()
Пример
Прозводится залп из двух орудий. Найти вeроятность P(C) поражения цели, если события A и B - соответственно попадание первым и вторым орудием - независимые события
C = (A + B), P(A)= 0.7, P(B) = 0.8
Подставляя получим P(A+B) = 0.7 + 0.8 - 0.56 = 0.94
Тот же ответ мы получим, если используем следствие 1 , вытекающее из аксиомы 4
![]() = 1-0.3·0.2=0.94
= 1-0.3·0.2=0.94
Частные случаи теоремы сложения
А) несовместные события AB = V, P(AB)=0 P(A+B) = P(A) + P(B)
Б) совместные события
* зависимые события P(B)-P(B/A) , P(A+B) = P(A) + P(B) - P(A)P(B/A)
** независимые события P(B)=P(B/A)
Выражение для суммы трех событий получим, используя правила из алгебры событий.
Р(А+В+С) = Р[(А+В)+С] = Р(А+В) + Р(С) – Р(АС+ВС) =
= Р(А) +Р(В) – Р(АВ) + Р(С) - [Р(АС) + Р(ВС) - Р(АС. ВС)] =
= Р(А) +Р(В) + Р(С) - Р(АС) - Р(АВ) - Р(ВС) + Р(АВС).
Выражение для суммы n событий находится обобщением полученных результатов:
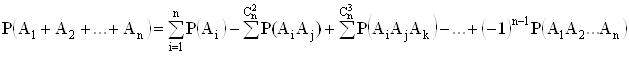 Частный случай: события независимы и Р(Аi) = р;
Частный случай: события независимы и Р(Аi) = р;
![]() .
.
Пример1:
Радиопередатчик выходит в эфир, в течение короткого промежутка времени передает сообщение и выключается. Для контроля эфира используется 4 независимых идентичных радиоприемных пунктов. Какова вероятность обнаружения работающего передатчика при работе всех радиоприемных пунктов (событие А) , если вероятность обнаружения на одном р=0,9 ?
![]()
- 6p2= 4p + 4p3 – p4 =
Какой должна быть вероятность обнаружения на одном приемном пункте, чтобы все вместе они обеспечивали вероятность обнаружения 0.9999
P(Ai) = ?
1.7.4 Теорема о вероятности появления хотя бы одного из независимых событий
Пусть событие А есть сумма событий ![]() , где все события независимы. Тогда
, где все события независимы. Тогда
![]() .
.
Теорема: Вероятность появления хоты бы одного из независимых событий равна разности между единицей и произведением вероятностей противоположных событий.
Доказательство: Предварительно покажем, что
![]() ;
;
Как следует из алгебры событий
![]()
Событие А, равносильное наступлению хотя бы одного из независимых событий ![]() , соответствует по определению их сумме
, соответствует по определению их сумме ![]() .
.
![]()
![]() =
=![]() .
.
Частный случай, который соответствует условиям задачи:
![]()
![]()
Применительно к условиям задачи об обнаружении работы передатчика получим
0,9999 = 1 – (1-Р)4 = 1 - q4; q4 = 0,0001; q = 0,1; p = 1 – q = 0,9.
Пример 2:
Вероятность поражения самолета одной ракетой равна p. Найти вероятность поражения при одновременном пуске трех ракет, считая, что поражение цели любой из ракет есть независимые события.
Два варианта решения
1. P(A+B+C) = P(A)+P(B)+P(C) - P(AB)-P(AC)-P(BC) + P(ABC)
2. P(A+B+C) = 3p - 3p2 + p3
P(A+B+C) = 1 - qn = 1 - q3 = 1 - (1-p)3
До сих пор мы рассматривали свойства вероятностей сумм и произведений событий. На практике появление или не появление интересующего нас события может быть связано с несколькими взаимно исключающими условиями.
1.7.5 Формула полной вероятности
Пусть событие А может происходить с одним из событий Н1, Н2, … , Нn. Эти события составляют полную группу несовместных событий. Вероятности появления каждого из них известны:
Р(Н1), Р(Н2), … , Р(Нn).
Поскольку неизвестно, с каким из событий Ні появилось событие А, то эти события называются гипотезами. Условные вероятности появления события А - Р(А/Ні) – известны.
Теорема: Вероятность события А, которое может наступить при появлении одного из полной группы несовместных событий – гипотез равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность события А
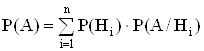 .
.
Доказательство: А = АН1 + АН2 + … + АНn - несовместны;
Р(А) = Р(Н1)Р(А/Н1) + Р(Н2)Р(А/Н2) + … + Р(Нn)Р(А/Нn).
Пример: В урне находится два шара, и в неё бросают белый шар. Затем наугад извлекают один шар. Найти вероятность извлечения белого шара (событие А), считая равновозможными следующие гипотезы:
Н1 – в урне два белых, Н2 – в урне два черных, Н3 – в урне черный и белый шары, Р(Н1) = Р(Н2) = Р(Н3) = 1/3.
Условные вероятности :
Р(А/Н1) = 1, Р(А/Н2) = 1/3 , Р(А/Н3)= 2/3
![]()
Проверка : 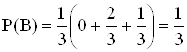 , В - извлечен черный шар.
, В - извлечен черный шар.
| < Предыдущая | Следующая > |
|---|