16. Числовые характеристики системы случайных величин
Моментом порядка (K,S) cистемы (X, Y) называется математическое ожидание произведения
![]() .
.
Для дискретных случайных величин
![]() если ряд сходится абсолютно.
если ряд сходится абсолютно.
Для непрерывных случайных величин  , где
, где
![]() - плотность распределения системы (X, Y), если интеграл существует.
- плотность распределения системы (X, Y), если интеграл существует.
Пример 3. Моментом порядка (1, 0) является математическое ожидание случайной величины X, а моментом порядка (0, 1) – математическое ожидание случайной величины Y. Cовокупность (MX, MY) геометрически представляет собой координаты средней точки на плоскости, вокруг которой происходит рассеивание вектора (X, Y).¨
Центральным моментом порядка (K, S) cистемы (X, Y) называется математическое ожидание произведения ![]()
![]() .
.
Пример 4. Центральным моментом порядка (2, 0) является дисперсия X, а центральным моментом порядка (0, 2) – дисперсия Y. DX и DY характеризуют рассеивание вектора (X, Y) в направлении осей ОХ и ОY. ¨
Момент порядка (1,1) ![]() называется Ковариацией случайных величин X и Y.
называется Ковариацией случайных величин X и Y.
Утверждение 1. Ковариацию можно считать по формуле ![]()
Доказательство:
![]() §
§
Утверждение 2. Дисперсия суммы случайных величин X и Y равна
![]() .
.
Доказательство.
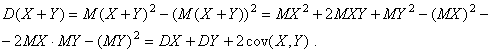 §
§
Коэффициентом корреляции случайных величин X и Y называется ![]() , где
, где ![]() – средние квадратические отклонения случайных величин X и Y.
– средние квадратические отклонения случайных величин X и Y.
![]() Пример 5. Посчитаем ковариацию и коэффициент корреляции случайных величин Х и Y из примера 1. Введем случайную величину Z=X*Y.
Пример 5. Посчитаем ковариацию и коэффициент корреляции случайных величин Х и Y из примера 1. Введем случайную величину Z=X*Y.
Z 0 1 MX= 1/2, DX=1/4, MY=3/4, DY=3/16, MZ=M(X*Y)=1/4;
Р 3/4 1/4 Cov(X, Y)=M(XY)-MX*MY= -1/8;
Corr(X, Y) = Cov (X, Y)/(sXSY) = –1/(![]() ). ¨
). ¨
Дисперсия суммы случайных величин X иY ![]() =
=
= 1/4+3/16+2*(-1/8) = 3/16.
| < Предыдущая | Следующая > |
|---|