17. Зависимость и ковариация

Cлучайные величины X и Y называются Независимыми, если функция распределения cлучайного вектора (X, Y) равняется произведению функций распределения компонент X и Y:

.

Утверждение 3. Непрерывные случайные величины независимы тогда и только тогда, когда плотность случайного вектора (X, Y) равняется произведению плотностей компонент X и Y: .

Для доказательства необходимости продифференцируем по X и Y обе части равенства из определения независимых случайных величин. Для доказательства достаточности возьмем интегралы от обеих частей равенства по области {(-¥, X), (-¥, Y)} §

Утверждение 4. Дискретные случайные величины независимы тогда и только тогда, когда для любых пар значений , случайных величин X и Y.

Доказательство.

§

Пример 6. В примере 1 § 1 плотность случайного вектора (X, Y) , а плотности компонент .

Следовательно, cлучайные величины X и Y независимы. ¨

Утверждение 5. Для независимых случайных величин X и Y ковариация равна 0.

Доказательство. Из утверждений 2 и 3 следует, что для независимых случайных величин X и Y M(XY) = M(X) × M(Y), если M(X) и M(Y) существуют.

Для непрерывных случайных величин это так, поскольку

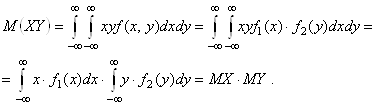
Для дискретных случайных величин

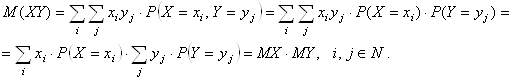
Отсюда, сov(X, Y) = M(XY) – M(X)M(Y) = 0. §

Замечание. M(XY) = M(X) × M(Y) также, если одна из независимых случайных величин непрерывного, а другая дискретного типа.

Таким образом, ненулевая ковариация - это признак наличия зависимости между случайными величинами.

Утверждение 6. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих случайных величин.

Доказательство сразу следует из формулы для дисперсии суммы случайных величин. §

< Предыдущая		Следующая >