15. Cиcтемы случайных величин. Распределение системы случайных величин

Пусть Х = (Х1, Х2,…,ХN) – cовокупность (или система) случайных величин.

Функцией распределения системы случайных величин называется вероятность совместного выполнения неравенств , , K = 1, 2, ..., N.

Свойства функции распределения аналогичны свойствам функции распределения одномерной случайной величины. Например, для системы двух случайных величин X и Y:

1) F(х, у) – неубывающая функция своих аргументов;

2) ;

3) , где F1(X), F2(Y) – функции распределения компонент X и Y;

4) .

Пример 1. Бросают две игральные кости. Cлучайная величина X принимает значение 1, если сумма выпавших очков четна, и равняется 0, если сумма нечетна. Cлучайная величина Y принимает значения 1 или 0, если произведение выпавших очков четно или нечетно. Совместное распределение (X, Y) можно задать в виде таблицы.

X  Y	0	1	Распределение Y
0 1	0 1/2	¼ ¼	1/4 3/4
Распределение X	1/2	½

Функция распределения вектора (X,Y)

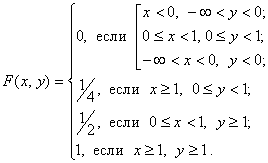
Функции распределения компонент: ¨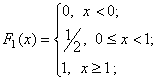

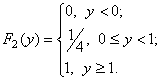Если функция распределения F(х, y) системы случайных величин (X,Y) дифференцируема, то ее вторую смешанную частную производную называют Плотностью распределения , Вектор (X, Y) в этом случае называют Непрерывным случайным вектором. Отсюда, .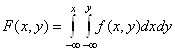

Cвойства плотности распределения непрерывного случайного вектора вытекают из свойств функции распределения:

1) ;

2) .

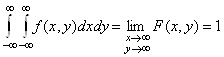3) т. к. , то .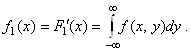

Замечание. Чтобы найти вероятность попадания непрерывного двумерного случайного вектора в область D, надо аналогично одномерному случаю проинтегрировать двумерную плотность распределения по области D:

.

Пример 2. Распределение двумерной случайной величины задается плотностью

(распределение Коши).

Найдем функцию распределения F(X, Y):

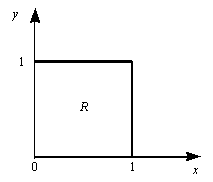Определим вероятность попадания случайной точки (X, Y) в квадрат R.

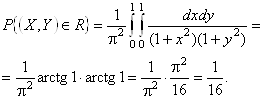
Плотность компоненты X

, .¨

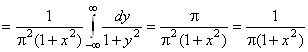< Предыдущая		Следующая >