08. Функция распределения случайной величины
Функцией распределения случайной величины Х называется функция F(X),
определяемая на всей действительной прямой как ![]() .
.
Замечание. Поскольку вероятность определена только на множествах из алгебры ![]() , не любую числовую функцию Х(w), w Î W, можно считать случайной величиной, а только ту, для которой множества {w: X(w) £ X}принадлежат алгебре
, не любую числовую функцию Х(w), w Î W, можно считать случайной величиной, а только ту, для которой множества {w: X(w) £ X}принадлежат алгебре ![]() при любом действительном X. Такие функции называются измеримыми.
при любом действительном X. Такие функции называются измеримыми.
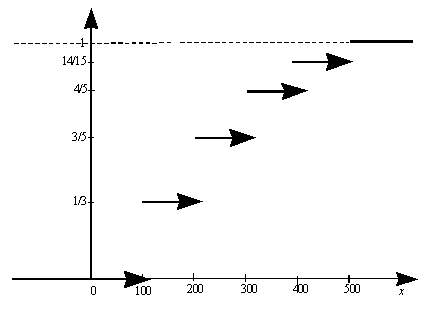 |
Пример 3. Построим график функции распределения случайной величины из примера 1.
Перечислим свойства функции распределения случайной величины.
Утверждение 1. F(X) не убывает.
Доказательство. Пусть Х1 < Х2. F(X2) – F(X1) = Р(X £ X2) – Р(X £ X1) =
= Р{w: X1< X(w) £ X2) ³ 0. Cледовательно, F(X1) £ F(X2). §
Утверждение 2. Функция F(X) непрерывна справа, т. е. ![]() .
.
Доказательство. Предположим, F(X) не является непрерывной справа в некоторой точке А: для ![]() F(А + d) - F(A) > 0, т. е. P{w: А < Х(w) £ A + d } > 0. Значит, с ненулевой вероятностью случайная величины Х принимает значения, которые превосходят А, но не превосходят А + d сразу для всех d. Но это невозможно, т. к. любое значение Х0 ,Большее A, будет превосходить и A + d при некоторых d.§
F(А + d) - F(A) > 0, т. е. P{w: А < Х(w) £ A + d } > 0. Значит, с ненулевой вероятностью случайная величины Х принимает значения, которые превосходят А, но не превосходят А + d сразу для всех d. Но это невозможно, т. к. любое значение Х0 ,Большее A, будет превосходить и A + d при некоторых d.§
Утверждение 3.![]() Будем считать это утверждение аксиомой. §
Будем считать это утверждение аксиомой. §
Замечание. Иногда рассматривают распределения, у которых ![]() Такие распределения называются Несобственными. Их изучение выходит за рамки нашего курса.
Такие распределения называются Несобственными. Их изучение выходит за рамки нашего курса.
| < Предыдущая | Следующая > |
|---|