07. Случайные величины. Дискретные случайные величины

Если задано некоторое вероятностное пространство (W, , Р), то под случайной величиной будем понимать числовую функцию X, заданную на пространстве W.

Cлучайные величины будем обозначать большими латинскими буквами, а значения, которые они принимают – соответствующими малыми.

Различают дискретные, непрерывные случайные величины и случайные величины с сингулярным распределением.

Дискретной называется случайная величина, принимающая конечное или счетное число различных значений.

Пример 1. Колесо рулетки разделено на 5 секторов, площади которых относятся как 5:4:3:2:1. Величина выигрыша пропорциональна номеру сектора, наименьший выигрыш –100 рублей.

Будем считать выигрыш случайной величиной Х. Это дискретная случайная величина. Она принимает значения: X1 = 100, X2 = 200, …, X5 = 500. ¨

Ecли мы укажем, c какими вероятностями дискретная случайная величина принимает свои значения, то мы зададим Распределение случайной величины.

Распределение дискретной случайной величины можно задать в виде таблицы.

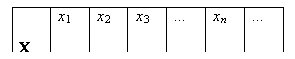В верхней строчке таблицы указываются значения случайной величины, а в нижней - вероятности этих значений. Вероятность значения случайной величины – это вероятность множества тех элементарных исходов, на которых случайная величина принимает это значение: P(Х = Хn) = Р{w: Х(w) = Хn}.

Пример 2. Случайная величина Х из примера 1 принимает свои значения со следующими вероятностями: Р1 = 5/15, Р2=4/15,…, Р5=1/15.

¨

< Предыдущая		Следующая >