§5. Несобственные интегралы, зависящие от параметра. Определение несобственного интеграла

Определение: Функция F называется локально интегрируемой, если , т. е. F – интегрируема на сегменте.

Определение: Пусть , пусть . Рассмотрим полуинтервал . Пусть задана функция . Будем считать, что локально интегрируема по переменной X на . Несобственным интегралом с особой точкой B по называется формальное выражение:.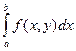

Определение: Будем говорить, что интеграл 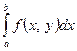сходится равномерно на множестве Q к I, если справедлива оценка 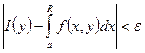или справедлива оценка 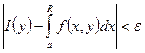. (Определение поточечной сходимости).

Пусть имеются два N-мерных пространства ; Пусть – предельная точка множества причем: Будем говорить, что равномерно стремится к при по если [Окрестность точки] , справедлива оценка . Обозначение следующее: .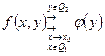

< Предыдущая		Следующая >