§5.2. Свойства несобственного интеграла, зависящего от параметра

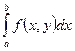Пусть – локально интегрируемы по X на . Пусть . и 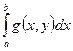сходится равномерно на Q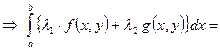

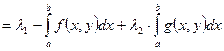– первое свойство несобственного интеграла, зависящего параметра, называющееся теоремой о линейности.

Теорема 2.2 (Замена переменных в несобственных интегралах, зависящих от параметра):

Пусть:

2. – непрерывна по X на .

3., при .

Тогда следующий интеграл сходится равномерно на множестве Q, тогда и только тогда, когда 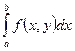сходится равномерно на множестве Q, причем справедливо равенство: .

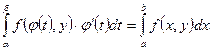Теорема 2.3: Пусть для каждого функции и по переменной X. Пусть Тогда 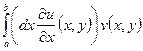сходится равномерно по тогда и только тогда, когда сходится равномерно по , причем верно: .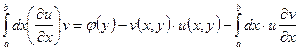

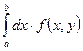Теорема 2.4: Пусть функция локально интегрируема по X на сегменте . Пусть сходится поточечно на множестве Q сходится равномерно на Q , тогда выполняется условие .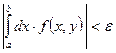

Док-во: Обозначим 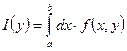при .

Заменим 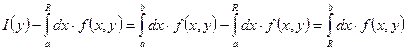– остаток.

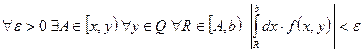, ч. т.д.

Теорема 2.5 (Критерий Коши): Пусть функция локально интегрируема по . 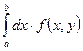сходится равномерно на Q тогда и только тогда, когда что выполняется условие .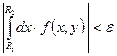

Док-во:

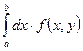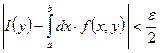1. Пусть сходится равномерно на множестве Q к функции I. Фиксируем . Выберем . Фиксируем мы можем записать следующее:

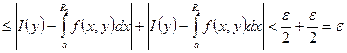. Необходимость выполнена.

2. Докажем достаточность. Пусть выполнено условие (1). Из этого следует, что 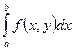сходится поточечно по критерию Коши. Фиксируем и выберем число , . Перейдем к пределу при . При этом 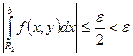. По теореме (2.4) 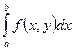сходится равномерно на Q, ч. т.д.

Теорема 2.6 (Признак Вейерштрасса): Пусть функция локально интегрируема по X. Пусть – локально интегрируема по X. Пусть:, при . Здесь . Пусть сходится интеграл 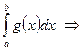интегралы 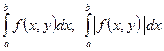– сходятся равномерно на Q.

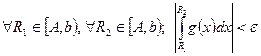Док-во: Без ограничения общности будем считать, что . Выберем Фиксируем . . Согласно критерию Коши интегралы 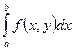и 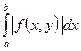сходятся равномерно на Q, ч. т.д.

Теорема 2.7 (Признак Дирихле-Абеля): Пусть функции и локально интегрируемы по . Пусть выполняются два требования:

1. ;

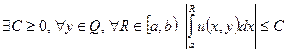2. функция монотонна по переменной X.

Тогда рассматриваемый интеграл сходится равномерно на Q.

Док-во: функция непрерывна по X; функция по X. Пусть: ( – рассматривается аналогично). Выберем .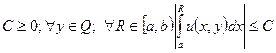

Фиксируем . Рассмотрим случай, когда – не возрастает по X; .

Фиксируем .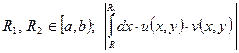

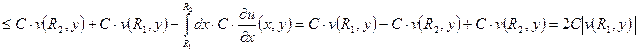. Пусть – не убывает по X, . Справедлива та же оценка. По условию теоремы, функция при монотонно равномерна по Y, следовательно, 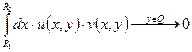при . По критерию Коши интеграл 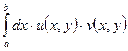сходится равномерно на множестве Q, ч. т.д.

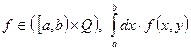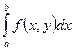Теорема 2.8 (Признак Дини): Пусть множество Пусть: сходится поточечно на Q к ; . Пусть либо либо , следовательно, сходится равномерно на множестве Q.

Док-во: Выберем . Обозначим: .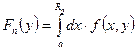

Согласно Теореме 1.2 . Так как 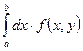– сходится поточечно, то , , – монотонная. Согласно признаку Дини для последовательности: . Покажем, что 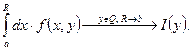Перепишем это . Положим . Фиксируем 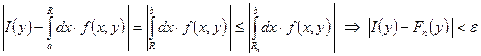, ч. т.д.

< Предыдущая		Следующая >