§5.3. Непрерывность, интегрирование и дифференцирование интеграла, зависящего от параметра

Теорема 2.9 (Непрерывность): Пусть: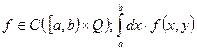 – сходится равномерно по Y на множестве Q к функции , следовательно, верно: .

Док-во: Выберем . Обозначим 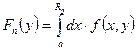, . Так как , ч. т.д.

Теорема 2.10 (Интегрируемость): Пусть: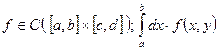 сходится равномерно на к функции I. Пусть . Обозначим следовательно:

1. – непрерывная функция;

2. ; причем сходится равномерно по ;

3. 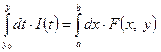, причем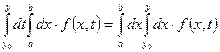

Док-во: Согласно Теореме 2.9:.

Согласно Теореме 1.2: , .

Нужно доказать: .

.

Используем Теорему 1.3 (об интегрировании собственного интеграла):

.

;

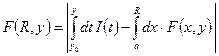Фиксируем : 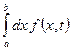сходится равномерно по T на

.

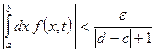Фиксируем , получим

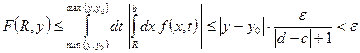, ч. т.д.

Теорема 2.11: Пусть и пусть существует при . Пусть . Пусть : сходится. Пусть 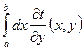сходится равномерно на к .

Тогда:

1. 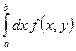сходится равномерно по Y на сегменте к некоторой функции , а также .

2. .

Док-во: В силу Теоремы 2.9 о непрерывной зависимости интеграла, зависящего от параметра можно записать:

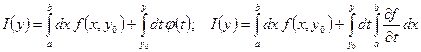
Согласно Теореме 2.10 во втором интеграле мы можем поменять местами интегралы:

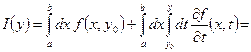(свойство линейности) –

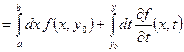Сходится равномерно по Y на сегменте . по формуле Ньютона-Лейбница:

.

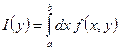Таким образом, интеграл 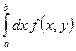сходится равномерно по Y на сегменте .

Так как , то , такая:

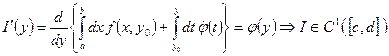
Следовательно, I – дифференцируемая функция, ч. т.д.

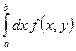Теорема 2.12: Пусть и интеграл сходится равномерно по Y на каждом сегменте к функции .

Пусть 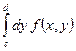сходится равномерно по Y на каждом сегменте к функции .

Пусть существует хотя бы один и .

Тогда:

1. 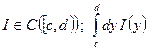– сходится.

2. – сходится.

3. или в следующем виде .

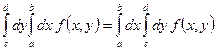Док-во: Пусть существует 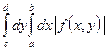. Без ограничения общности будем считать, что . Используя Теорему 2.9, получаем, что и . Поскольку сходится поточечно, то мы можем оценить функцию следующим образом:

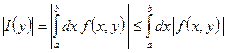. По признаку сравнения интеграл сходится, также 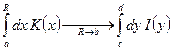. Докажем этот факт, введя следующую функцию :

.

Согласно Теореме 2.10 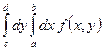сходится.

.

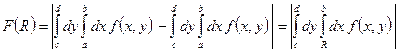Фиксируем , следовательно, мы можем записать:

.

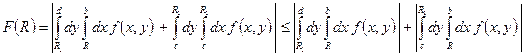
По признаку Вейерштрасса интеграл 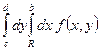сходится равномерно по R на сегменте . Фиксируем . Выберем : .

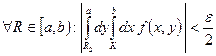Заметим, что интеграл сходится равномерно по Y на сегменте (по условию теоремы). Можно указать , что .

Фиксируя , ч. т.д.

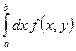Теорема 2.13 (Третья теорема об интегрировании): Пусть интеграл сходится поточечно на к функции ; , 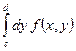сходится поточечно на к функции ; . Пусть далее или , существует один из интегралов или . Тогда существует из них и они равны друг другу.

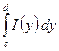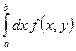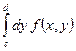Док-во: Пусть существует и без ограничения общности будем считать, что . Согласно признаку Дини (Теорема 2.8) сходится равномерно на любом сегменте . Тогда интеграл сходится равномерно на : ; либо –1. Следовательно, существует . Тогда, согласно Теореме 2.12, сходится 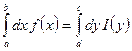, ч. т.д.

< Предыдущая		Следующая >