§6.3. Однопараметрическое семейство кривых
![]() , где
, где ![]() - некоторый параметр.
- некоторый параметр.
I ![]()
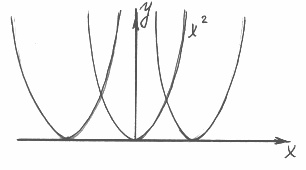
II ![]()
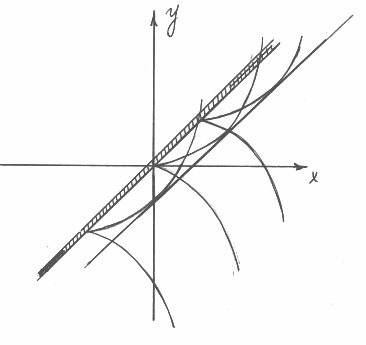
(Жирная заштрихованная прямая – является особой прямой, т. е. прямой состоящей из особых точек.)
Остальные кривые рассматриваемого семейства получаются из кривой ![]() , в результате параллельного переноса (или параллельного сдвига) вдоль биссектрисы I и III четвертей.
, в результате параллельного переноса (или параллельного сдвига) вдоль биссектрисы I и III четвертей.
Точка ![]() называется характеристической точкой однопараметрического семейства кривых, если
называется характеристической точкой однопараметрического семейства кривых, если
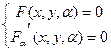
Отвечающей данному значению a.
Опр. Огибающей однопараметрического семейства кривых называется кривая, которая:
1) в каждой своей точке касается только одной кривой данного семейства
2) в разных своих точках касается различных кривых указанного семейства.
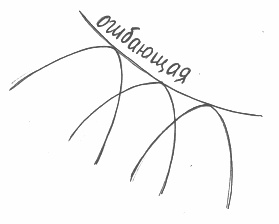
Опр. Дискриминантной кривой называется кривая реализующая собой геометрическое место характеристических точек на плоскости.
Лемма 1
Пусть точка ![]() - характеристическая точка однопараметрического семейства
- характеристическая точка однопараметрического семейства ![]() , отвечающая a=0.
, отвечающая a=0.
Пусть функция ![]() и функция
и функция ![]() являются дифференцируемыми функциями в некоторой окрестности точки
являются дифференцируемыми функциями в некоторой окрестности точки ![]() и их частные производные по переменным x, y непрерывны в самой точке
и их частные производные по переменным x, y непрерывны в самой точке ![]() , тогда, если в точке
, тогда, если в точке ![]() якобиан
якобиан
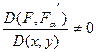 (в точке
(в точке ![]() ), то
), то
Дискриминантная кривая, проходящая через точку М0, в некоторой окрестности этой точки может быть задана параметрически, как функция параметра a.
![]() ,
,
Где функции j и y дифференцируемы в некоторой окрестности ![]() .
.
Теорема 1
Пусть выполнены все условия леммы 1, кроме этого, выполнены следующие условия:
В некоторой окрестности точки ![]()
![]() являются непрерывными функциями.
являются непрерывными функциями.
В точке ![]() выполняются соотношения
выполняются соотношения ![]() и
и ![]() .
.
Тогда дискриминантная кривая, проходя через точку ![]() , является в некоторой окрестности этой точки огибающей.
, является в некоторой окрестности этой точки огибающей.
Пример:
I ![]()
![]()
Для нахождения характеристических точек запишем условие:
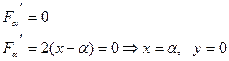
![]()
Проверим условия сформулированной теоремы.
![]()
![]()
Тогда, дискриминантная кривая, согласно сформулированной теореме, представляет собой ось X и является огибающей.
II ![]()
Рассмотрим семейство полукубических парабол и найдем дискриминантную кривую
![]()
![]()
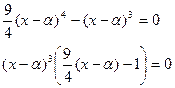
1) ![]()
2) 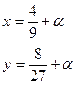
(убедиться самостоятельно, что прямая, получающаяся в 1), не является огибающей, а в 2) – является огибающей семейства кривых)
Вычислить частные производные, указанные в теореме: в первом случае они обращаются в нуль, а во втором - нет.
| < Предыдущая | Следующая > |
|---|