§5.6. Упрощенный вариант формулы Грина

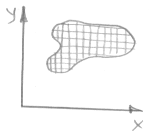
1. G- простая область.

2. На ¶G задано направление обхода таким образом, чтобы при движении на этом направлении область оставалась слева.

3. P,Q Î C1(G)- гладкие.

Тогда справедлива формула Грина.

И справедливы два равенства отдельно.

Док-во:

1) Пусть G- Y- трапециевидная область

Докажем для нее утверждение:

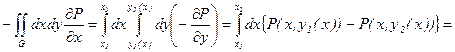
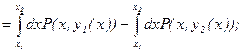
l1: y=y1(x), x1£X£X2

x=x,

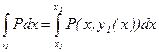
L2: y=y, y1(x2)£Y£Y2(x2)

x=X2

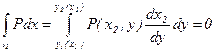(так как X2=Const)

L3: y=y2(x)

x=x, x1£X£X2

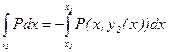
L4: y=y, y1(x1)£Y£Y2(x1)

x=X1

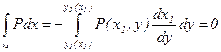(так как X1=Const)

Þ -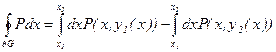

Это совпадает с тем, что мы получили для двойного интеграла

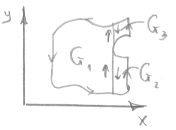
2) Пусть G- простая область.

Опираясь на результат, полученный в первом пункте, докажем формулу

Gk- у - трапециевидная область, K¹N :

Gk И Gn не имеют общих внутренних точек,

(т. е. )

=конечное число дуг.

Запишем двойной интеграл.

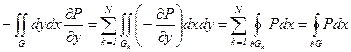
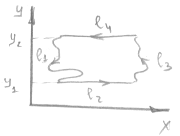
3) Пусть G- X – трапециевидная область.

Доказательство аналогично пункту 1.

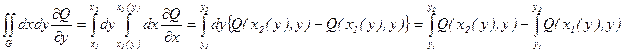
С другой стороны

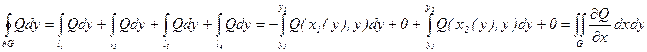
4) G- простая область. Докажем, что

= конечное число дуг.

Ч. т. д.

§7. Теорема о независимости криволинейного интеграла второго рода от пути интегрирования

G- открытая область;

P,Q Î С(G).

Предположим

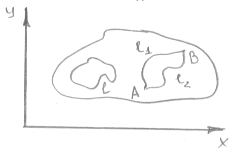
1)

2) Предположим, что

(А не зависит от формы пути).

l - кусочно-гладкая замкнутая кривая

L1, L2 – кусочно-гладкие.

3) Предположим

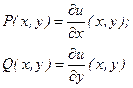
Предположения (1), (2), (3) эквивалентны друг другу.

Док-во:

(1) Þ (2) Þ (3) Þ (1)

Доказать самостоятельно.

ч. т. д.

Теорема

Предположим, что P,Q Î C1(G) – гладкие

4) Предположим:

Тогда из (3) Þ (4)

Док-во

Ч. т. д.

Опр. 4: G- линейно-связанное множество, если любые две его точки можно соединить непрерывной дугой

Опр. 5: G- односвязное множество, если оно

1) линейно связано;

2) любые две кривые, целиком лежащие и с общими концами, можно непрерывно продеформировать одну в другую.

Теорема

Если G- односвязная область, а функции P И Q Î C1(G) – гладкие, то из (4) Þ (1)

-не только необходимое, но и достаточное условие или условие интегрируемости.

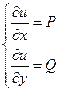
Док-во:

Применим формулу Грина.

ч. т. д.

Переход (1) Þ (2).

Можно заменить каждую из произвольных дуг на ломаную так, чтобы интеграл не изменился.

Переход (2) Þ (3)

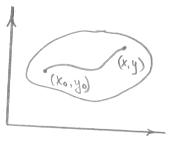
(X0,Y0)- Фиксированные.

(х, у) – "

Используя теорему о среднем.

< Предыдущая		Следующая >