§5.5. Формула Грина

Теорема

1) G Í R2- замкнутая ограниченная область на плоскости.

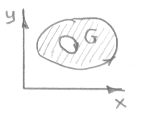
¶G состоит из конечного числа замкнутых кусочно-гладких кривых.

2) Пусть на границе задано направление обхода, причем таким образом, чтобы область оставалась слева.

3) P,Q Î C1(G)- гладкие.

Тогда справедлива формула Грина.

Можно сказать иначе.

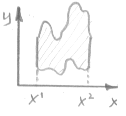
Опр. 1: G- Y – трапециевидная область, если это замкнутая ограниченная область,

Причем её можно представить в виде криволинейной трапеции:

G={(X,Y):X1£X£X2;Y1(X)£Y£Y2(X)},

Y1,Y2- кусочно-гладкие кривые.

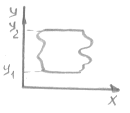
Опр. 2: G- X – трапециевидная область, если это замкнутая ограниченная область, представимая в следующем виде.

G={(X,Y):Y1£Y£Y2;X1(Y)£X£X2(Y)}

х1,X2 –кусочно-гладкие кривые

Опр. 3: G- простая область, если

1) G можно разбить на конечное число Y-трапециевидных областей;

2) При этом G можно также разбить и на конечное число Х- трапециевидных областей.

< Предыдущая		Следующая >