§5.4. Криволинейные интегралы второго рода
![]()
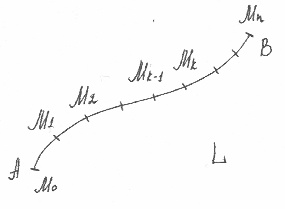
Также, как и раньше устроим разбиение кривой L
![]()
![]()
Пусть на кривой L заданы две функции: ![]()
Составим следующие интегральные суммы:
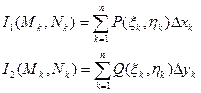
Для указанных сумм Im, M =1,2 аналогичным образом вводится понятие интегральной суммы.
Пределы интегральных сумм обозначим:
I1 , I2
Если указанные пределы интегральных сумм существуют пределы интегральных сумм, то они называются криволинейными интегралами второго рода:
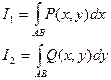
При этом вводится понятие общего криволинейного интеграла второго рода:
![]() ,
,
Где знак интеграла относится ко всему выражению.
Замечание:
Для криволинейных интегралов второго рода справедливо следующее свойство:
![]() .
.
RN [a, b]
{x(t)} Î C1([a, b])
A1(x).. aN(x)


| < Предыдущая | Следующая > |
|---|