§5.3. Правило вычисления криволинейных интегралов первого рода

Опр.: Кривая L Называется гладкой на сегменте , если производные , функций , являются непрерывными на сегменте и не равняются нулю одновременно.

Опр.: Кривая L называется кусочно гладкой, если для нее выполняются все требования гладкой кривой за исключением конечного числа точек.

Опр.: Функция F(M) = F(X, Y) называется непрерывной вдоль кривой L, если

.

Опр.: Функция F(M) Называется кусочно непрерывной вдоль кривой L, если для нее выполнены все требования непрерывности за исключением конечного числа точек, в которых функция имеет разрыв первого рода.

Теорема

Пусть L является кусочно гладкой кривой, а функция F(X,Y) – кусочно непрерывная функция вдоль кривой L. Тогда существует следующий криволинейный интеграл первого рода, вычисляемый по формуле

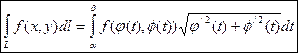
Замечания.

1) В том случае, если L является частью графика функции, тогда

,

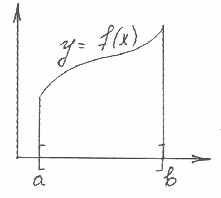
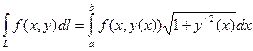- параметрическое задание

2) Допустим, что , задана в полярных координатах

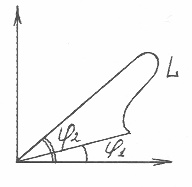
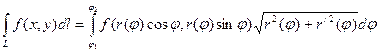
Замечание:

В трехмерном случае криволинейный интеграл вводится совершенно аналогичным образом:

В этом случае:

Пример:

Вычислить криволинейный интеграл первого рода:

L – астроида:

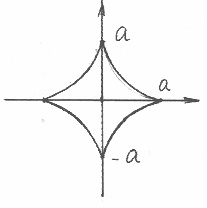
Параметрическое уравнение астроиды:

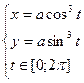
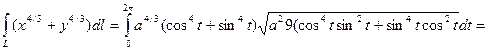
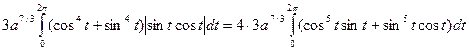
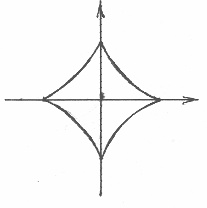
То, что рассматриваемая область состоит из четырех одинаковых фрагментов еще, не является достаточным условием для перехода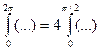

Достаточным условием такого перехода является то, что и значения функции на всех идентичных сегментах будут совпадать.

< Предыдущая		Следующая >