§4. Приближенные методы вычисления определенных интегралов

В методе прямоугольников приближенное вычисление интеграла происходит с точностью до h3. В методе трапеций заменяем площадь исследуемой фигуры площадью трапеции. Точность та же – до h3. Метод парабол: заменяем f(x) параболой, проходящей через три точки. Этот метод более точен, чем предыдущие, хотя он тоже дает точность порядка h3.

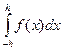
Вспомогательное утверждение:

Пусть f(x) непрерывна на [a, b], тогда:

(1)

Где x Î [a, b], а x1 ,x2, …. xn соответствуют некоторому T[a, b].

Пусть m, M – соответственно точная нижняя и верхняя грани функции на [a, b].

Тогда выполняются неравенства:

А, следовательно,

Так как функция непрерывна, то она может принимать любые произвольные значения между m и M:

$xÎ[a, b]:

< Предыдущая		Следующая >