§3.17. Замена переменных в кратных интегралах

Опр.: RN: A Í RN.

Будем говорить, что А- область, если А - большое, непустое, открытое множество.

Опр.:. А- замкнутая область, если А ¹ Æ .

Опр.: А- регулярное множество (Reg [A,RN]), если А¹Æ .

Y: RN1 ® RN2

Y(t)=(Y1(t).. YN2(t)), t=(t1,...tN1).

Опр.: Матрицей Якоби назовем матрицу

Если N1=N2 Þ матрица квадратная Þ $ определитель

.

Отображение Y:RN1®RN2

Отображение J:RN2®RN3

N1=N2=N3=N

Теорема о замене переменных

Пусть:

А- измеримое множество,

J- интегрируемая функция на этом множестве. (Т. е. J Î R(A)).

A* – измеримое множество.

S Í A,

A\S- открытая (не равное пустому множеству) область.

S* Í A*, .

A*\S*- область.

Y: RN®RN

Y Î C1(A*\S*)

Y взаимно однозначно отображает A*\S* на A\S

При T Î A*\S*.

при T Î A*\S*.

F- ограниченная на A*.

Тогда F Î R(A*) и

Пример:

Перейдем к полярным координатам:

х=RCosJ, R³0, 0£J£2P

у=RSinJ

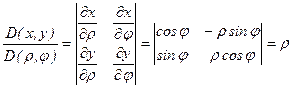
R = 0 (якобиан превращается в 0).

Второй вариант теоремы

Пусть:

А- замкнутая область,

J Î C(A),

A*­­-замкнутая область.

Y: RN® RN,

Y Î C1(A*),

Y взаимно однозначно отображает А* на А.

При T Î A*.

Тогда

, и

Док-во:

1) Докажем теорему только для линейного отображения

Формулировка

Лемма 1

Пусть:

А- измеримое множество.

J Î R(A).

A*- измеримое множество.

T- матрица M´N.

Det(T)¹0

Тогда

{J(Tt)|det(T)|}Î R(A*)

и справедлива формула А=T´A*

Доказательство в Ильине, Позняке.

ч. т. д.

Обозначения:

||T||- норма точки

||T||- норма матрицы .

||Tt||£||T|| ||T||.

- функция отображения.

R(C)={X Î RN: ||x-Y(T0)||£MS}

Используя теорему о неявной функции можно показать, что

Y(int(G))=int(Y(G)).

Y(¶G)=¶Y(G).

G- замкнутый куб.

S(C)- 0,5 длины стороны.

C={t Î RN: ||t-t0||£S}

Лемма 2

Пусть выполнены все условия теоремы.

(1) C Í A*- замкнутый куб.

Тогда образ замкнутого куба при отображении Y(С) Î R(C)

(2) Если G- измеримое множество,

.

Y(G)- измеримое множество (т. е. замена переменных сохраняет измеримость, но в том случае, когда).

(3) Если С- замкнутый куб;

С Í int(A*),

То M(Y(С))£(M(C))NM(C)

Докажем лемму:

(1) C Í A*

Фиксируем T Î C,

Y(t)- Y(t0)=Du Y(X)(t-t0)

X - промежуточная точка.

|| Y(t)- Y(t0)||£||DuY(X)|| ||t-t0||

Y(C) Î R(C)

m(R(C))=(M(C))N m(C)

Докажем (2).

G Î int(A*)

Y(G) Î A Þ Y(G) ограничено.

Чтобы доказать измеримость, нужно доказать ¶Y(G) имеет меру 0.

Q- замкнутый куб.

А* Í Q

Qk-замкнутые кубы

K- множество таких номеров, что

По построению, очевидно, что

¶G Í D Þ ¶Y(G)=Y(¶G)£

(граница образа совпадает с образом границы)

.

Qk Í A* (если разбиение достаточно мелкое).

Дальше будем считать, что Qk Í Int(A*).

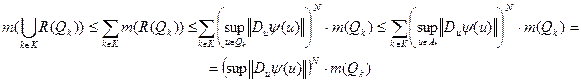
M(D) ® 0 При D({Qk})®0

При D({Qk})®0

-следовательно, оно измеримо.

(3) C Í int(A*)

Y(С) Î R©, M(Y©)£M(R©)=(M©)N M©

ч. т. д.

Лемма 3

Пусть G- измеримое по Жордану множество.

Тогда

Доказательство(с помощью оценок, полученных в первой лемме) в Ильине-Позняке.

ч. т. д.

Доказательство теоремы о замене переменных.

Каждый интеграл содержит неотрицательную функцию (докажем для них)

Без ограничения общности: J(х) ³0 при Х Î A

Q- замкнутый куб.

А Í Q

Рассмотрим множество номеров K1, что

При

-прообраз Qk

При D({Qk})®0.

С другой стороны, воспользуемся леммой 2

Т. к. Mk=inf Þ

Функция неотрицательная Þ можно аппроксимировать дальше

.

Переходя к пределу получаем такую оценку:

.

В нашем случае A И A* взаимозаменяемы и все условия вообще выполняются

Применим те же рассуждения не к функции J(х), а к функции G(T). Получаем:

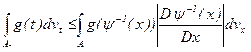
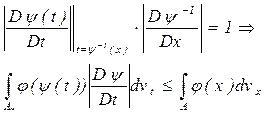
Две встречных оценки могут выполняться, только если есть точное равенство Þ

(смотри второй том Ильина - Позняка).

ч. т. д.

Составим интегральную сумму для такого разбиения

Заменим параллелограмм S=Произведению векторов

- это производная нашей функции по первой переменной.

- это производная нашей функции по второй переменной.

 

< Предыдущая		Следующая >