§4.1. Метод прямоугольников

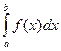
Пусть T[a, b] – равномерное разбиение сегмента [a, b] на n элементарных сегментов

[x2k-1; x2k], k = 1, …, n.

На каждом элементарном сегменте выберем некоторую произвольную точку, принадлежащую сегменту, и вычислим значение функции в данных точках:

X2k-1Î [x2k-1; x2k], f(x1), f(x3), …. f(x2k-1)

Тогда сумма всех значений

Определенный интеграл может быть представлен в виде:

,

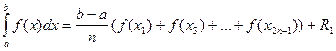Где R1 – остаточный член.

Докажем, что методе прямоугольников остаточный член имеет вид:

(2)

Примечание: предполагается, что функций f(x) имеет непрерывную вторую производную на [a, b].

Док-во

Рассмотрим вспомогательный интеграл

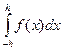
Пусть F(x) является первообразной функции f(x) на [a, b].

Тогда F(x) имеет непрерывную третью производную на [a, b].

(3)

(по формуле Ньютона-Лейбница).

Разложим F(x) в ряд Тейлора в точке 0.

Остаточный член запишем в форме Лагранжа:

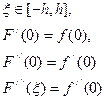
Вернемся к формуле (3):

=

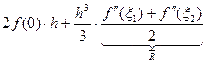
Рассмотрим остаточный член

(x1x2Î [-h, h])

Формула (1)

(HÎ[-H,H])

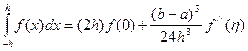(4)

(HÎ[-H,H])

Таким образом, получена формула для приближенного вычисления интеграла на отдельном элементарном сегменте [-h, h]:

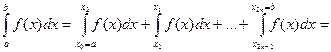
(Для каждого из интегралов в правой части справедливо соотношение типа (4))

 

По формуле (1), F(X), где XÎ[A,B]

Таким образом получено:

Тем самым, получена приближенная формула, позволяющая вычислять интегралы методои прямоугольников.

< Предыдущая		Следующая >