§3.04. Некоторые классы интегрируемых функций

Обозначения (в лекциях Бадьина):

J-функция

D(J)-область определения функции

R(J)-область значений функции

X, y - некоторые множества

J:x®Y-функция J действует из множества X в множество Y

\-разность множеств

-пересечение множеств

-объединение множеств

[a, b]={tÎR: min{a, b}£T£Max{a, b}}

(a, b]=[a, b]\{a}

(a, b)=[a, b]\{a, b}

JÎR([a, b])- функция, интегрируемая на сегменте [a, b]

J ÎC([a, b])- функция, дифференцируемая на сегменте

J Î C1([a, b])-сама функция дифференцируемая и ее первая производная дифференцируема на сегменте

Q Í R-множество Q полностью лежит в множестве R

- последовательность интервалов, где K изменяется от 1 до N

M(I) – мера Жордана

-замыкание множества

Int (D) – внутренняя часть множества

¶D – граница множества D

Û - тогда и только тогда, когда.

Опр.: Q Í R. Q называется множеством нулевой длины, если " E > 0 можно указать такую конечную последовательность интервалов (AK<BK), покрывающая рассматриваемое множество, т. е. , а

Теорема

Пусть A¹B; Q – множество точек разрыва J - ограниченная функция на [a, b], а множество её точек разрыва имеет не нулевую длину. Тогда J Î R([a, b]).

Док-во:

Без ограничения общности, рассмотрим случай, когда A<b покажем, что J удовлетворяет критерию интегрируемости.

Фиксируем произвольное E > 0.

Рассмотрим (AK<BK), такую, что она покрывает множество , а

.

Используя A, b,AK,BK построим разбиение [a, b] , такое, что

K2={1…N1}\K1

Рассмотрим сегмент [xk-1,xk], k Î K2.

Здесь нет точек разрыва по построению Þ непрерывна Þ (по теореме Кантора) она равномерно непрерывна Þ ,;

-колебания.

(доказать самостоятельно)

Колебание – разность между точными гранями.

- более мелкое разбиение, обладающее следующими свойствами:

1. ;;

2. на оставшихся сегментах

Составим разность между суммами Дарбу.

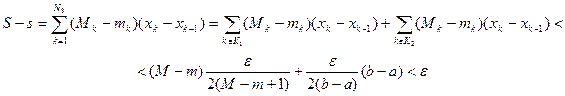
ч. т. д.

Следствие: Если j непрерывна на сегменте [a, b], то она интегрируема на сегменте [a, b], т. е. A ¹ b, J Î C([a, b]) Þ J Î R([a, b]).

Утверждение 2: Пусть A ¹ b; J - ограниченная, монотонная функция Þ эта функция интегрируема по Риману, т. е. J Î R([a, b]).

< Предыдущая		Следующая >