§3.05. Свойства определённого интеграла
1. A, b Î R; J Î R([a, b]), L Î R. Тогда LJ Î R([a, b])
![]()
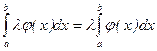
2. J1, J2 Î R([a, b]). Тогда J1+J2 Î R([a, b])
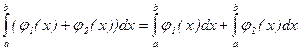
Утверждение 3: Предположим, что J1, J2 Î R([a, b]). Тогда {J1(x) J2(x)} Î R([a, b]).
Док-во:
(основано на критерии Дарбу)
Без ограничения общности, будем считать, что A<b.
Фиксируем E >0; фиксируем некоторое разбиение ![]()
Рассмотрим [xk-1,xk]
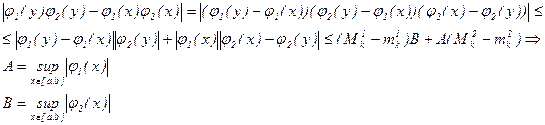
M-m = sup|J(y)-J(x)|
![]()
![]()
Выберем разбиение {xk}
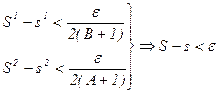
ч. т. д.
Утверждение 4: Предположим, что [a1,b1] Í [a, b]; J Î R([a, b]) Þ J Î R([a1,b1]).
Доказательство самостоятельно (используя суммы Дарбу).
Утверждение 5: Пусть J Î R([a, b]); J Î R([b, c]) Þ J Î R([a, c]), причём
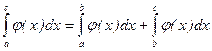
Доказательство самостоятельно
| < Предыдущая | Следующая > |
|---|