§3.03. Свойства сумм Дарбу

1. по всем .

по всем .

2. Пусть T2 получено из разбиения T1 добавлением некоторого числа точек (измельчением), тогда для сумм Дарбу, отвечающим разбиению T2:

3. Нижняя сумма Дарбу произвольного разбиения не превосходит верхней суммы Дарбу любого другого разбиения.

4. 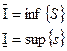(sup и inf берутся по всем возможным разбиениям)

называется нижним (верхним) интегралом Дарбу.

5. Лемма Дарбу:

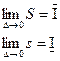
Теорема 1

Для того, чтобы функция , ограниченная на сегменте , была интегрируемой, необходимо и достаточно, чтобы

.

Теорема 2

Для того, чтобы функция , ограниченная на сегменте , была интегрируемой, необходимо и достаточно, чтобы , такое что

, или

,

Где ,

-колебание функции на сегменте .

Примеры:

1) Функция Дирихле

Выясним вопрос, является ли функция Дирихле интегрируемой на сегменте .

На каждом элементарном сегменте разбиения имеются как рациональные, так и иррациональные точки.

Не существует такого , чтобы .

2) Функция Римана

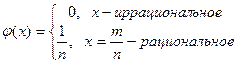
Докажем, что функция Римана является интегрируемой.

Докажем, что функция Римана удовлетворяет

(*)

Только для конечного числа точек.

Все рациональные точки сегмента (т. е. точки вида ) можно занумеровать. Сначала занумеруем точки . Значение функции в этой точке равно 1.

Их конечное число-это целые точки сегмента .

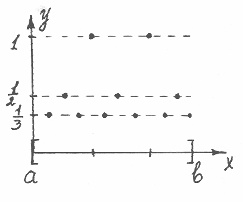
Занумеруем точки и . Чем ниже уровень, тем точек становится больше. В число N указанных точек, удовлетворяющих условию (*), попадут те точки, в которых , т. е.

(**)

Если N удовлетворяет условию (**), то это те точки, для которых выполняется (*).

Покроем N указанных точек системой попарно перекрывающихся сегментов, общая сумма длин которых не превышает . Длины этих сегментов обозначим .

Таким образом получаем некоторое разбиение.

На сегменте колебания функции не превышают единицы. Имеется также некоторое количество остальных сегментов , колебания функции на которых

.

Выше уравнения будет располагаться конечное число точек, которые будут вносит основной вклад в интегральную сумму

Таким образом функция Римана является интегрируемой на сегменте .

 

< Предыдущая		Следующая >