§3.14. Теория кратных интегралов

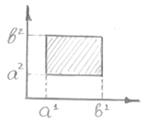
RN ;Q-невырожденный параллелепипед.

Q={ (X1..,XN) : A1£X1£B1 .. AN£XN£BN }

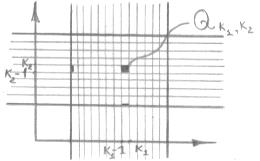
Построим разбиение

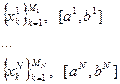
- весь набор индексов

J(x1..xN)

S - интегральная сумма (по всем возможным индексам)

-разбиение

-промежуточные точки

Опр.: J называется пределом, если для любого E>0 $ D>0: ", " , если

D- диаметр разбиения

Если существует предел интегральных сумм, то функция интегрируема.

Для введения определения

(1) A- измеримое множество Þ A- ограничено.

A Í Q

Предположим, что J(x) задано на A.

Доопределим.

(2) A- измеримое множество.

Предположим, что ; Аk - измеримое :Ak, An при K¹N не пересекаются.

XK Î Ak

Теорема

Функция интегрируема по первому определению Û она интегрируема по второму определению и пределы совпадают. Оказывается, что

< Предыдущая		Следующая >