§3.13. Мера Жордана. Кратные интегралы
Опр.: Мера Жордана – длина на прямой, площадь на плоскости, объём в пространстве.
I Í R
I ¹ Æ I=[a, b]
I=(a, b], J=[a, b)
J=(a, b)
Обозначим m(J) =b-a
J = Æ Þ m(J)=0
Рассмотрим RN, N³2
Q Í RN: x1 Î J1, … , xn Î Jn, где J1, … , Jn – связанные, ограниченные.
M(Q)=m(J1)…m(Jn)
M(Q)³0
D Í RN
, где Qk – параллелепипед; 
D – элементарная фигура
M(D) не зависит от того, каким способом разбиваем параллелепипед, и называется мерой Жордана для элементарной фигуры.
 |
D1,D2 – элементарные фигуры Þ
- элементарные фигуры.
D – элементарная фигура Þ 
, Int(D), ¶D-элементарные фигуры.
M(¶D) = 0; 
M(int(D))=m(D)
A-ограниченное множество.
Рассмотрим все возможные элементарные фигуры.
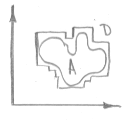
A Í D
- множество всех фигур, описывающих A
- верхняя мера Жордана множества A
У " ограниченного множества есть 
D Í A
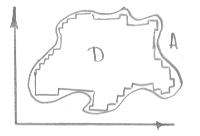
-множество всех вписанных в A фигуру
-нижняя мера множества A (есть у " ограниченного множества)
Опр.: Множество A называется измеримым по Жордану, если оно ограниченно и
Обозначим M(A) - мера Жордана измеряемого множества M(A)>0
A1,A2-измеримые множества Þ 
- измеримые множества.
A1-измеримое множество
A2 получено из A1 параллельным переносом и поворотом Þ M(A2)=m(A1)
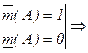Множество не измеримо по Жордану.
Теорема
Множество A измеримо по Жордану Û для " E >0 можно указать такие элементарные фигуры D1 И D2, что
D1 Í A Í D2; m(D2)-m(D1)<E, т. е.
" E >0 $ D1, D2: D1 Í A Í D2:
m(D2)-m(D1)<E.
Док-во:
1. Пусть A – измеримо Þ A –ограниченно Þ 
Фиксируем E > 0.
Выберем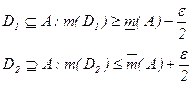 
Þ m(D2)-m(D1)<E
2. E > 0; D2, D1; m(D2)-m(D1)<E.
Т. к. E произвольно, то Þ A – измеримо по Жордану.
Ч. т. д.
Теорема
A – измеримо по Жордану Û оно ограничено, и мера границы = 0, т. е. 
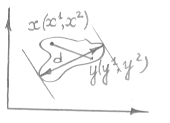
Вспомогательное утверждение:
A – измеримо;
Ak – измеримо
Обозначение:
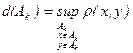- диаметр множества.
A({Ak})=Max(D(Ak))
B Í A, 
.
Тогда " E > 0 $ D > 0: " {Ak}, если D({Ak}) < D, то
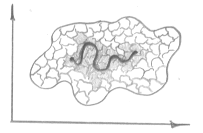
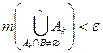
Доказательство теоремы:
1. Предположим, что
A - Измеримое Þ A- ограничено.
Согласно 1-ой теореме Вейерштрасса можно указать
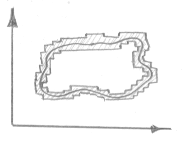
D1 Í A, A Í D2
E > 0
M(D2)-m(D1)<E
=M(D2)-m(D1)<E (по построению)
Þ 
2.Предположим, что
A ограничено, и
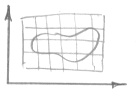
Значит всегда можно указать параллелепипед Q.
Фиксируем E>0.
Используя утверждение, построим разложение Q
;
Qk параллелепипеды, такие, что
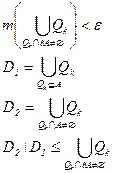
(по построению)
Согласно предыдущей теореме A- измеримо.
Ч. т. д.
| < Предыдущая | Следующая > |
|---|
