§3.15. Теорема о сведении двойного интеграла к повторному

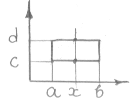
A<b, c<d; Q={(x, y):a£X£B, c£Y£D}

J(x, y) интегрируема на Q

Предположим, что для каждого X Î [a, b] J(x, y) интегрируема по переменной Y на [c, d].

Тогда функция вида

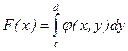
Интегрируема на [a, b], причем

Док-во:

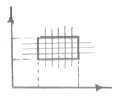
Построим разбиение {xk­}[a, b].

XK Î [xk-1,xk]

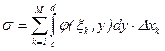
S - интегральная сумма для внешнего интеграла по форме {yn} [c, d].

D ({yn})£D({xk})

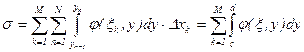
Тогда справедлива оценка для (x, y) Î Qk, n

Mk, n£J(x, y)£Mk, n

Мы воспользовались, что

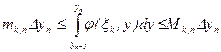
s£S£S (для двойного интеграла)

S-нижняя сумма Дарбу для двойного интеграла .

S- верхняя сумма Дарбу для двойного интеграла .

Если D({xk})®0, То D({Qk, n})®0.

ч. т. д.

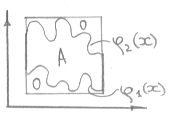
Формула для криволинейной трапеции.

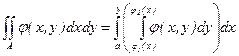
Доопределяем нулями.

< Предыдущая		Следующая >