§2.4. Неявные функции, задаваемые системой уравнений

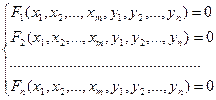(3)

Будем предполагать, что система (3) задает неявные функции:

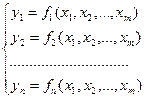(4)

Функции (4) называются совокупностью неявных функций, определяемых системой (3).

Рассмотрим определитель:

(5)

Определитель Якоби или якобиан.

Теорема 2.

Пусть:

1) - дифференцируемы в некоторой окрестности точки

2) Все частные производные - по аргументам непрерывны в .

3)

якобиан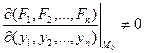

Тогда существует такой параллелепипед из точек

где

Целиком лежащий в окрестности В котором система (3) задается единственной совокупностью неявных функций типа (4), таких что

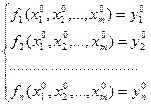
Кроме того функции - дифференцируются при .

А частная производная вычисляется по следующей методике.

Допустим для системы (3) найдено, отвечающая ей совокупность неявных функций (4). «Подставим» неявные указанные функции в систему (3), в результате подстановки система (3) обратиться в систему тождеств, которые можно продифференцировать на найденных неявных функциях.

Продифференцируем каждое тождество по переменной

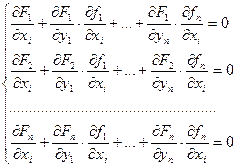(6)

Нам нужно найти

Система (6) представляет собой систему линейных уравнений для нахождения частных производных. Система (6) рассматривается на неявных функциях.

Вычислим определитель левых частей

Искомые частные производные являются решениями системы (6) как системы линейных уравнений по формулам Крамера.

Пример:

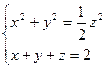
Из этого следует, что точка имеет координаты

Найти:

Перепишем в другом виде

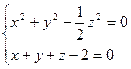
Проверим выполнение условий теоремы (2).

1) Функция дифференцируема.

2)

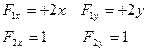
Согласно теореме неявные функции существуют. Подставим неявные функции в систему и продифференцируем.

Для нахождения вторых производных продифференцируем систему .

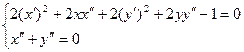
< Предыдущая		Следующая >