§1.20. Частные производные высших порядков
Опр. Функция ![]() называется n раз дифференцируемой в некоторой точке
называется n раз дифференцируемой в некоторой точке ![]() , если все частные производные n-1 порядка являются дифференцируемыми в точке
, если все частные производные n-1 порядка являются дифференцируемыми в точке ![]() .
.
Достаточное условие дифференцируемости
Функция ![]() является n раз дифференцируемой в некоторой точке
является n раз дифференцируемой в некоторой точке ![]() , если все частные производные функции U n-1 порядка являются непрерывными в точке
, если все частные производные функции U n-1 порядка являются непрерывными в точке ![]() .
.
Теорема (о независимости смешанных производных от порядка дифференцирования)
Пусть функция ![]() дважды дифференцируема в некоторой точке
дважды дифференцируема в некоторой точке ![]() , тогда справедливо следующее соотношение:
, тогда справедливо следующее соотношение:
![]() (в точке
(в точке ![]() )
)
Док-во:
Рассмотрим вспомогательное выражение
![]()
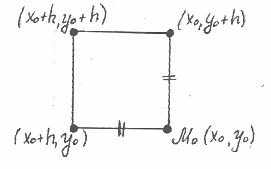
Функция Ф(x) может быть рассмотрена, как приращение вида:
Где ![]() .
.
Функция является дифференцируемой функцией на
Сегменте ![]() , поэтому по формуле Лагранжа для функции одной переменной
, поэтому по формуле Лагранжа для функции одной переменной
![]()
Тогда на рассматриваемом сегменте есть такая точка, что
![]() , где 0<θ<1
, где 0<θ<1
Добавим и вычтем ![]() в точке
в точке ![]() .
.
![]()
Поскольку функция дифференцируема, то ее приращение пропорционально приращению аргумента
![]() ,
,
Где ![]() -бесконечно малые при
-бесконечно малые при ![]() .
.
Второй раз применим формулу Лагранжа.
Аналогичным образом выражение Ф представимо, как приращение функции ψ.
![]() , где
, где ![]()
Процедура стереотипна.
Получается следующее выражение:
![]() - 1 случай
- 1 случай
![]() - 2 случай
- 2 случай
Где ![]() - бесконечно малые.
- бесконечно малые.
Приравниваем и сопоставляем.
![]() - часть Ф порядка малости
- часть Ф порядка малости ![]() .
.
Ч. т. д.
| < Предыдущая | Следующая > |
|---|