§1.19. Производная по направлению. Градиент

Пусть рассматриваемая функция .

Рассмотрим некоторый единичный вектор , где

A, b, g - углы образованные единичным вектором с координатными осями декартовой системы координат.

Исследуем характер изменения функции , вдоль прямой с направляющим вектором . Тогда указанная прямая l, будет параметрически задаваться формулами:

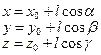
Функция в направлении прямой l представляет собой сложную функцию параметра .

По теореме о дифференцировании сложной функции вычислим производную по направлению.

Опр. Градиентом функции в точке М называется вектор следующего вида

Тогда производная по направлению

Скалярное произведение на .

,

Где j - угол образованный вектором градиента и .

Производная по направлению принимает max значение когда cosj=1, когда направляющий вектор прямой коллинеарен градиенту. Следовательно градиент функции указывает на направление наибольшего роста функции в данной точке.

В случае двух переменных, производная по направлению вычисляется по формуле:

< Предыдущая		Следующая >