§1.18. Дифференцирование сложных функций или функций зависящих от параметра

Рассмотрим (1)

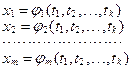(2)

Теорема (о дифференцировании сложной функции)

Пусть функция дифференцируема в точке N .

- дифференцируемы в точке М , при этом

Тогда функция (1) дифференцируема в точке М , и при этом выполняются следующие соотношения.

(3)

Док-во:

Т. к. функция дифференцируема в точке N, то ее приращение DU представимо в виде:

(4)

Функции при .

Т. к. функции определяемые (2) дифференцируемы в точке М, то

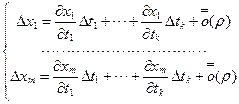, (5)

Где

.

Подставим выражение для из системы (5) в формулу (4).

В результате должно подучиться:

, Где

Общая формула:

,

Где i пробегает значения от 1 до K.

Функция дифференцируема в точке М, следовательно, коэффициентами при будут частичные производные т. е.

Ч. т. д.

< Предыдущая		Следующая >