§1.11. Понятие сложной функции

Будем предполагать

(*)

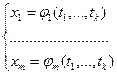Пусть функции заданы в некоторой области .

Пусть функции непрерывны в т. , при этом

(**)

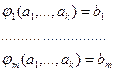Рассмотрим т. .

Пусть функция U=F(M) непрерывна в т. В.

Теорема 3 (о непрерывной сложной функции нескольких переменных)*

Пусть функции , определенные системой (*), непрерывны в некоторой т. К-мерного евклидова пространства .

При этом выполняются условия (**).

Пусть функция непрерывна в т. ,

Тогда функция непрерывна в т. А.

Доказано самостоятельно:

Нам требуется доказать, что

при .

В силу непрерывности функции : такое, что

при или

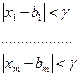
Воспользуемся тем, что являются непрерывными в т. А.

такое, что

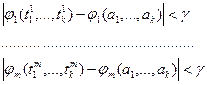при .

Но

,

…………………………………..

,

Значит, условие можно переписать как:

,

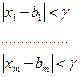при .

Следовательно, такое, что

при .

ч. т. д.

Теорема 4 (о прохождении функцией нескольких переменных любого промежуточного значения)

Пусть функция U=F(M) Является непрерывной в {M} (некоторой связной области {M}).

Пусть значение функции

, , где

произвольно выбранные фиксированные точки.

Пусть .

Тогда на непрерывной кривой L , соединяющей т. и целиком принадлежащей множеству {M} найдется такая т. , что F(M*)=C.

 

Док-во:

Рассмотрим некоторую кривую

, где .

L – соединяет т. .

Мы рассматриваем функцию .

Рассмотрим функцию U В некоторой точке, принадлежащей кривой L:

, при этом

.

Таким образом, получено параметрическое представление кривой, соединяющей т. .

U является сложной функцией параметра T: F(T) при условии .

По теореме о сложной функции F(T) является непрерывной на .

Пусть есть некоторая т. .

По соответствующей теореме для функции одной переменной существует такое значение

, что , т. е.

.

Выберем т. М* как точку, имеющую следующие координаты:

U(M*)=C.

ч. т. д.

< Предыдущая		Следующая >