§1.10. Теоремы о непрерывных функциях

Теорема 1*

Пусть функции U=F(M) и U=G(M) непрерывны в некоторой области, тогда

также являются непрерывными в данной области.

Доказано самостоятельно:

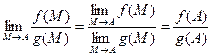
Следовательно, функции непрерывны в т. А, а т. А – любая точка из области, в которой непрерывны функции F(M) и G(M).

ч. т. д.

Теорема 2(о постоянстве знака непрерывной функции в окрестности некоторой точки)

Пусть U=F(M) непрерывна в т. А, пусть F(А) > 0, тогда:

выполняется условие: F(M)>0.

Док-во:

По определению непрерывной функции:

такое, что при выполняется условие: .

Выберем

Тогда

ч. т. д.

Замечание:

Аналогичным образом формулируется теорема, когда F(А)<0.

< Предыдущая		Следующая >