§1.09. Непрерывность функции по отдельной переменной
![]() .
.
Опр: Если ![]() При
При ![]() , то говорят, что функция непрерывна по переменной
, то говорят, что функция непрерывна по переменной ![]() .
.
Утверждение:
Из непрерывности функции по совокупности переменных следует её непрерывность по всем переменным. Обратное не верно.
Пример:
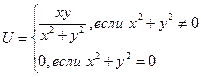
Повторные пределы функции существуют и равны 0 , т. е. совпадают со значением функции в данной точке.
Таким образом, функция является непрерывной по каждой переменой.
Но предел функции равен ![]() при
при ![]() . Следовательно, функция U=F(M) не является непрерывной в т. (0,0) по совокупности переменных.
. Следовательно, функция U=F(M) не является непрерывной в т. (0,0) по совокупности переменных.
| < Предыдущая | Следующая > |
|---|