18. Решение матричных уравнений

Система n линейных алгебраических уравнений относительно N неизвестных х1, х2, …, хn может быть записана в матричном виде ах=b где: .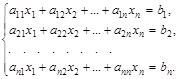

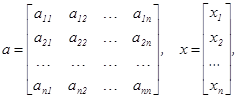
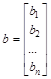Если матрица а – неособенная, то есть det(а) ¹ 0 то система, имеет единственное решение. Для решения систем линейных уравнений можно использовать общепринятые математические методы: метод Крамера, матричный метод и т. д.

Системы линейных уравнений удобно решать с помощью функции lsolve(а, b) – где а – матрица коэффициентов (не сингулярная), b – вектор свободных членов.

19.

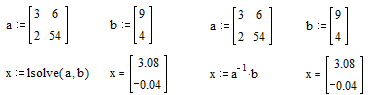Решение дифференциальных уравнений и систем

Основные функции

Для решения дифференциальных однородных дифференциальных уравнений (ОДУ) – с начальными условиями пакет Mathcad имеет ряд встроенных функций:

1. rkfixed – функция решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

2. Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

3. Bulstoer –функция решения ОДУ и систем ОДУ методом – метод Булирша–Штёра если заранее известно, что решением является гладкая функция.

Рассмотрим подробнее каждую из этих функций:

1. rkfixed(y, x1, x2, p, D) – Возвращает матрицу первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – решения, первые n-1 производные. Функция возвращает матрицу, состоящую из 1+n строк. Аргументы функции: y – вектор начальных условий (k элементов); x1 и x2 – границы интервала, на котором ищется решение ОДУ; p – число точек внутри интервала (x1, x2), в которых ищется решение; D – вектор, состоящий из k элементов, который содержит первые производные искомой функции.

2. Rkadapt(y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed. Существует несколько модифицированная функция rkadapt(y, x1,x2, acc, p,D, k,s) – где добавлены параметры k – максимальное число промежуточных точек решения; s – минимально допустимый интервал между точками; acc – погрешность решения (рекомендуется порядка 0.001).

3. Bulstoer(y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed.

Рекомендации по использованию

Обычно функция Rkadapt благодаря автоматическому изменению шага решения дает более точный результат, но по скорости вычислений она проигрывает функции rkfixed, хотя если решение меняется медленно, она может привести к заметному уменьшению числа вычислений. Поэтому функция Rkadapt наиболее пригодна для решения ОДУ дающих медленно меняющееся решения.

< Предыдущая		Следующая >