17. Нахождение корней полинома

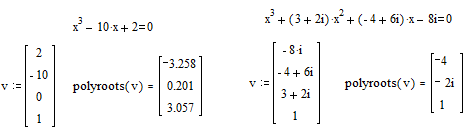
Для нахождения корней выражения, вида используется функция polyroots. В отличие от функции root, polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Общий вид polyroots(v), где v – вектор коэффициентов полинома длины , n – степень полинома. Возвращает вектор длины N, состоящий из корней полинома. Вектор v удобно создавать использую команду меню Symbolics – Polynomial Cofficients.

Решение систем уравнений и неравенств

MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.

Наиболее распространенным является блочный метод. Mathcad решает систему с помощью итерационных методов. Для решения системы этим методом необходимо выполнить следующее:

1. Задать начальное приближение для всех неизвестных, входящих в систему уравнений;

2. Напечатать ключевое слово Given. Оно указывает, что далее следует система уравнений;

3. Введите уравнения и неравенства в любом порядке. Используйте [Ctrl] + = либо палитру, для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, ³ и £;

4. Введите любое выражение, которое включает функцию Find, например: .

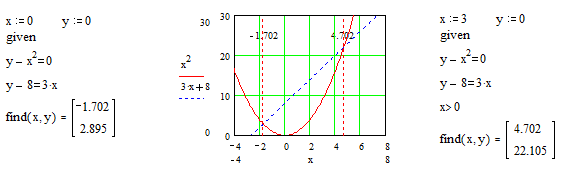
Mathcad возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Решающим блоком – называется часть документа, расположенная между ключевыми словами Given и Find. Внутри блока недопустимы следующие символы: ¹, дискретные переменные или выражения, содержащие дискретный аргумент в любой форме, неравенства вида a<b<c, вложенные блоки решения уравнений.

Функция, Find может возвращать результат следующими способами:

1. Find(var1, var2,…) =.

2. a := Find(x) – скаляр, var := Find(var1, var2,…) – вектор. Удобно при использовании решения системы в другом месте рабочего документа.

3. f(a, b, c, …) := Find(x, y, z, …). Определить другую функцию с помощью Find. Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений;

4. f(x, y, z, …) := Find(x, y, z, …).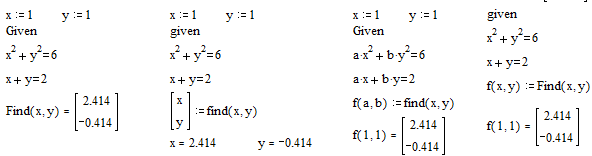
Если необходимо найти решение при различных начальных приближениях, имеет смысл определить новую функцию.

Последние два способа можно комбинировать.

Отсутствие сходимости решения

Сообщение об ошибке (Решение не найдено) при решении уравнений появляется, когда:

1. система не имеет решения;

2. для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот;

3. в процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения;

4. возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL.

Приближенные решения

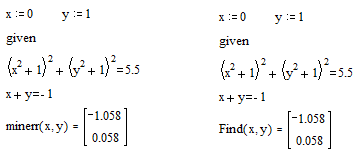Функция Minerr очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find. Общий вид Minerr Minerr(z1, z2, ...). Число аргументов должно быть равно числу неизвестных. При использовании Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.

< Предыдущая		Следующая >