3.08.5. Некоторые оценки хроматического числа

Уже отмечалось, что χ(Кn) = n. Поэтому если граф G содержит полный подграф порядка R, то χ(G) ≥ r. В целом, чем меньше ребер в графе и чем меньше степени его вершин, тем меньше хроматическое число.

Теорема. Пусть R – минимальная степень вершин графа G, тогда существует правильная (R+1)–раскраска графа G.

Доказательство. Индукция по числу вершин N графа G.

База индукции: N = 2 -- утверждение очевидно.

Индукционный переход. Предположим, что существует правильная (R+1)–раскраска для всех графов порядка N, у которых степени вершин не превосходят R. Рассмотрим граф порядка N+1 с максимальной степенью вершин, равной R. Удалим произвольную вершину . Для полученного графа порядка N существует согласно индукционному предположению правильная (R+1) – раскраска. Воспользуемся такой раскраской. Удаленная вершина имеет не более R смежных, для окраски которых использовано не более R цветов. Окрасим вершину в цвет, отличный от цвета смежных вершин (так как цветов больше, чем R, то такой цвет найдется). Получим правильную (R+1)–раскраску исходного графа.

Теорема (Брукс). Пусть G – связный граф, не являющийся полный, и степени всех вершин которого не превосходят R, где R ≥ 3. Тогда χ(G) ≤ r.

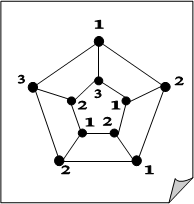
Замечание. Оценка хроматического числа в теореме Брукса достижима (см. рисунок) и, значит, не может быть в общем случае (без дополнительных предположений) улучшена. Однако, оценка весьма грубая. При выполнении условий теоремы хроматическое число может быть значительно меньше максимальной степени вершин. Например, звездный граф К1,N , и с максимальной степенью вершин N имеет хроматическое число 2. Для колеса W2N по теореме Брукса χ(W2N) ≤ 2N. В действительности χ(W2N) = 3.

< Предыдущая		Следующая >