3.08.4. Хроматическое число 2–дольного графа. Критерий 2-дольности

Предложение. Пусть G – некоторый непустой граф. Тогда χ(G) = 2 в том и только том случае, когда G -- 2–дольный граф.

Доказательство. Необходимость. Пусть χ(G) = 2. Обозначим через V1 все вершины графа G , раскрашенные в один цвет, а через V2 – в другой. Поскольку между вершинами, имеющими одинаковый цвет, нет ребер. То граф G – 2–дольный с долями V1 и V2.

Достаточность. Пусть G – 2–дольный граф. Окрасим вершины одной доли в один цвет, а другой доли – в другой цвет. Очевидно, полученная раскраска правильная и, значит, χ(G) = 2.

Теорема. (критерий 2-дольности). Граф двудольный тогда и только тогда, когда он не имеет циклов нечетной длины.

Доказательство. Необходимость. Пусть G – двудольный граф. Рассмотрим какой-нибудь цикл ( если он существует, иначе доказывать нечего). Поскольку ребра соединяют только вершины из разных долей графа, то двигаясь по циклу мы будем поочередно переходить из одной доли в другую, пока, наконец, не вернемся в исходную вершину ( и исходную долю). Поэтому цикл имеет четную длину.

Достаточность. Пусть все циклы в графе G имеют четную длину. Без потери общности можно считать, что G -- связный. И пусть – некоторая вершина графа G. Обозначим, через V1 – множество вершин графа G, расстояние от которых до вершины являются четными ( в частности ÎV1) , а через V2 – остальные вершины графа. Достаточно показать, что если вершины U,V1 (или V2), то они не являются смежными. Предположим противное, что существует ребро{U,}. Рассмотрим кратчайшие цепи S(U,) и S(,) между соответствующими парами вершин. Обе они имеют четную длину ( нечетную, если U, WV2). Тогда объединяя эти цепи и добавляя ребро {U, W} получим цикл нечетной длины. 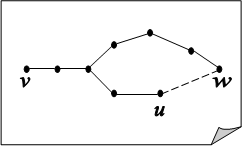Возможно, цепи S(U,) и S(,) имеют общие ребра (см. рисунок). Тогда цикл получится, если удалить их из описанного объединения. Очевидно, длина его остается нечетной. Полученное противоречие завершает доказательство.

< Предыдущая		Следующая >