2.6.1. Предикаты. Основные понятия и определения
Рассмотрим высказывание: “X – простое число”. Подставляя вместо X конкретные числа: 3, 4, 5 и т. д., получим высказывания, которые в одних случаях будут истинными, а в других – ложными. Таким образом, данное высказывание определяет отображение, которое каждому натуральному числу X ставит в соответствие значение 0 ("ложь") или 1 ("истина").
Аналогично, высказывание “![]() ” определяет отображение R2®
” определяет отображение R2®![]() . Например, (1, 3) a 1, так как “1 < 3” – верное высказывание, а (4, 2) a 0, так как “4 < 2” – ложное высказывание.
. Например, (1, 3) a 1, так как “1 < 3” – верное высказывание, а (4, 2) a 0, так как “4 < 2” – ложное высказывание.
Определение. N-местным предикатом на множестве M называется отображение ![]() . Множество M при этом называется Предметной областью предиката
. Множество M при этом называется Предметной областью предиката ![]() , а Xi (I = 1, 2, …, N) – Предметными переменными. Множество N-ок
, а Xi (I = 1, 2, …, N) – Предметными переменными. Множество N-ок ![]() , для которых
, для которых ![]() называется Областью истинности предиката P.
называется Областью истинности предиката P.
Например, областью истинности предиката P(X, Y) =  , где X, Y Î R (предметная область – множество действительных чисел R), является множество точек
, где X, Y Î R (предметная область – множество действительных чисел R), является множество точек ![]() , которые на координатной плоскости образуют параболу.
, которые на координатной плоскости образуют параболу.
Определение. Предикат ![]() , который при всех возможных значениях предметных переменных принимает одно и то же значение 1 ( 0 ) называется Тождественно истинным (Тождественно ложным). Предикат, для которого существует набор
, который при всех возможных значениях предметных переменных принимает одно и то же значение 1 ( 0 ) называется Тождественно истинным (Тождественно ложным). Предикат, для которого существует набор ![]() , такой, что
, такой, что ![]() (т. е. множество истинности которого не пусто) называется Выполнимым.
(т. е. множество истинности которого не пусто) называется Выполнимым.
Определение. Два предиката ![]() и
и ![]() с одной и той же предметной областью M называются равносильными, если они принимают одинаковые значения при всех возможных значениях предметных переменных
с одной и той же предметной областью M называются равносильными, если они принимают одинаковые значения при всех возможных значениях предметных переменных ![]() (т. е., если P и Q равны как отображения).
(т. е., если P и Q равны как отображения).
Понятно, что два предиката равносильны, если их области истинности совпадают.
Всякому отображению ![]() можно поставить в соответствие (N+1)-местный предикат по следующему правилу:
можно поставить в соответствие (N+1)-местный предикат по следующему правилу:
P(A1, A2, …, An) = 
Существует также взаимно однозначное соответствие между N-местными предикатами с предметной областью М и N-арными отношениями на М. Действительно, всякому предикату ![]() можно поставить в соответствие отношение
можно поставить в соответствие отношение ![]() , такое, что
, такое, что ![]() , если
, если ![]() и только в этом случае. Обратно, всякому отношению
и только в этом случае. Обратно, всякому отношению ![]() отвечает N-местный предикат
отвечает N-местный предикат ![]() с предметной областью М, определяемый равенством:
с предметной областью М, определяемый равенством:
P(A1, A2, …, An) = 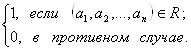
Таким образом, предикаты выражают свойства элементов предметной области М или отношения на М (см. примеры, предваряющие определение предиката).
| < Предыдущая | Следующая > |
|---|