2.5.2. Схемы из функциональных элементов

В настоящее время контактные схемы используются редко ввиду их невысокого быстродействия. Те же функции ù , Ù и Ú реализуются с помощью специальных элементов (полупроводниковых и др.), которые мы будем называть функциональными элементами.

Каждый Функциональный элемент имеет n упорядоченных входов и один выход. При каждом наборе сигналов на входах (1 – есть сигнал, 2 –нет) может возникнуть определенный сигнал (0 или 1) на выходе.

Примеры и обозначения функциональных элементов на схемах:

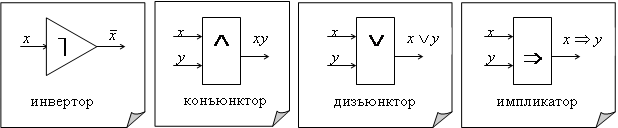Если имеется несколько функциональных элементов, то из них можно получить новые следующим образом.

1. Некоторые входы одного элемента соединить с входами других элементов (см. рис), что отвечает композиции соответствующих функций;

2. Объединить некоторые входы, что означает отождествление соответствующих переменных и приводит к функции с меньшим числом переменных.

Такие соединения функциональных элементов называются Допустимыми. Полученные в результате таких соединений, схемы также называются допустимыми.

Вход функционального элемента (или схемы) называется Фиктивным, если при любом наборе сигналов на других входах результат на выходе не зависит от сигнала на данном входе. В противном случае (если зависит), вход называется Существенным. Если рассмотреть функцию, отвечающую данному функциональному элементу, то существует пропозиционная формула, которая не содержит переменных, соответствующих фиктивным входам, и содержит все переменные, соответствующие существенным входам.

Соединения следующего вида, когда выход данного функционального элемента соединяется со входом, называются Недопустимыми. Схемы с такими соединениями (cм. рисунки) не смогут функционировать, если соответствующие входы являются существенными.

Пример 1. Синтезировать логическую схему, реализующую булеву функцию

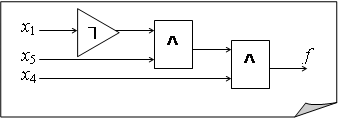Минимизируя в классе ДНФ, получим представление . Следовательно, здесь переменные X2, X3 – фиктивные, от них значение функции не зависит. Соответствующая схема показана на рисунке

Предположим, что эту же функцию нужно реализовать в базисе . Найдем соответствующую формулу. Отрицание, конъюнкция и дизъюнкция представляются через импликацию следующим образом:

Тогда

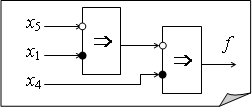Учитывая, что , полученную формулу можно упростить: Соответствующая схема изображена на рисунке.

При сборе схем с использованием импликаторов важно не перепутать входы. На схеме первые и вторые входы помечены и , соответственно.

Пример 2. Синтез N–разрядного сумматора.

Построим логическую схему, реализующую суммирование двух N–разрядных чисел, представляющих в двоичной системе исчисления. Пусть и -- два данных числа, где Xi и Yi – их цифры (0 или1). Пусть -- их сумма и -- число, цифры которого соответствуют переносам знаков в следующий разряд при обычном способе суммирования многозначных чисел.

Цифры Zi и переносы знака Pi, легко видеть, определяются следующими условиями

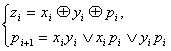
Если в распоряжении не имеется элементов, соответствующих сумме по модулю 2, то необходимо представить через конъюнкцию, дизъюнкцию и отрицание:

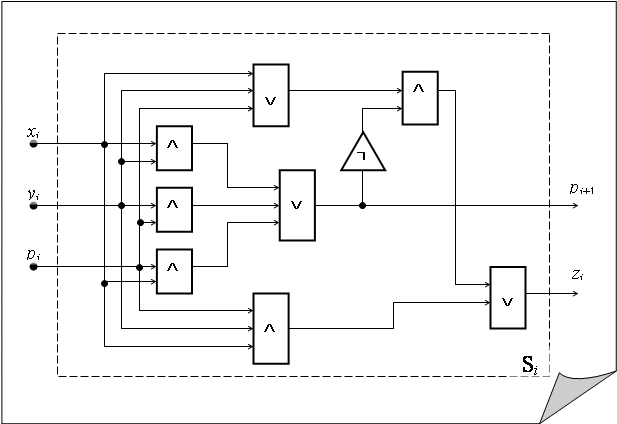На следующей схеме представлен одноразрядный сумматор Si, который на выходе выдает значения Zi и Pi+1 :

Общая схема сумматора выглядит следующим образом:

< Предыдущая		Следующая >