Лекция 03. Определение и способ задания булевых функций
Булевой функцией от n аргументов называется однозначное отображение n – мерного булева куба на одномерный булев куб.
Способы задания функций
1. Табличный
|
X1 X2 X3 … XN |
F(X) |
|
0 0 0 0 0 0 0 0 0 |
G1 |
|
… |
Gi |
|
1 1 1 1 1 1 1 1 1 |
Gn |
Gi - значение функции от данных аргументов.
Порядок возрастания векторов по мере возрастания их номеров называют лексикографическим.
2. Векторный
F = (g1...gn)
3. Геометрический
Единичным вектором для данной функции называется тот вектор, значение функции на котором равно 1.
Носителем данной функции – совокупность всех единичных векторов этой функции (Nf – носитель функции f)
На векторах, помеченных звездочкой, функция обращается в 1.
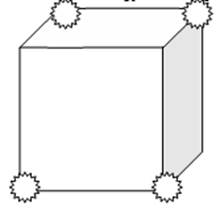
Nf = {001, 011, 100, 110} = [1,3,4,6] [] – указаны номера векторов.
3. В виде формулы.
Функция f зависит от переменной xi фиктивно, если для любых двух наборов значений переменных, отличающихся только значением переменной xi, значения функции f совпадают.
Будем говорить, что f зависит от переменной xi существенно, если существуют такие два набора значений, отличающихся только значением переменной xi, на которых значения функций различно.
Фиктивные переменные у функции можно добавлять и исключать.
Две булевы функции называются равными или равносильными, если одну можно получить из другой путем добавления и изъятия фиктивных переменных.
Строим таблицу функций при n = 1.
|
X |
0 |
X |
_ X |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
Таблица всех элементарных булевых функций, применяемых в записи формул
X |
Y |
0 |
& |
_____ Y®X |
X |
___ X®Y |
Y |
+ |
V |
¯ |
~ |
_ Y |
X ®Y |
_X |
Y®X |
/ |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Все эти функции от двух аргументов мы и будем называть элементарными булевыми функциями.
Основными элементарными функциями являются конъюнкция, дизъюнкция и отрицание.
Элементарные булевы функции удовлетворяют всем аксиомам булевой алгебры.
Суперпозиции булевых функций
Ф = {ф1…фk}
F называется элементарной суперпозицией функции из множества Ф, если она получена одним из следующих способов.
1. Переименование какого-нибудь аргумента в одной из функций системы (возможно отождествление аргумента).
2. В одну из функций системы вместо любого аргумента ставится значение любой функции из этой системы.
Ф1 = {Y…xn}
Фi = (x1 … фj(x1…xn) … xn)
Ф(1) – множество всех элементарных суперпозиций из системы Ф.
Ф(k+1) – множество всех элементарных суперпозиций из систему Фk.
Функция g называется суперпозицией функций из системы, если
$ N : g Î Фn
Это означает, что g можно получить из функции системы Ф, применяя конечное число раз операцию элементарной суперпозиции.
Конкретное выражение суперпозиции будем называть формулой над системой Ф.
G = Fф
Суперпозиция элементарных булевых функций – формула.
Для удобства записи договоримся, что отрицание – самая сильная операция. Следующая – конъюнкция, а остальные – равносильны.
_ _
X+Y = XY V XY
_ _
X ~ Y = XY V XY
__
X ® Y = X V Y
_ _
X ¯ Y = X Y
| < Предыдущая | Следующая > |
|---|